Зворотня задача вибору пропускних спроможностей

Це задача третього типу, описана в розділі 3.1. Потрібно знайти такий розподіл пропускних спроможностей мережі, які б задовольняли умовам по часу перебування в мережі (3.4) і при цьому мінімізували вартість капіталу (3.3). Отже, формально ця задача може бути записана у вигляді

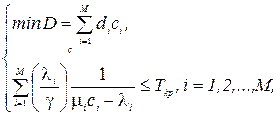
де Т_кр – фіксоване значення часу перебування в мережі, яке не може бути перевищено ні при якій доставці.

На відміну від попередньої задачі ця постановка трохи посилена. Тут вважається, що час обслуговування в кожному каналі розподілений по своєму експоненційному законі із середнім .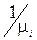

Складемо функцію Лагранжа

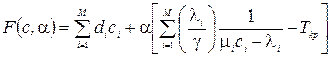. (3.13)

Візьмемо часткові похідні від (3.13), прирівняємо їх нулю і розв’яжемо рівняння відносно 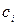. Отже,

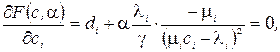i = 1,2,…,M. (3.14)

В розв’язку (3.14) нам невідоме значення невизначеного множника Лагранжа a. Для того, щоб його знайти, підставимо 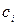з (3.14) в обмеження і розв’яжемо рівняння, що отримаємо, відносно a. Маємо

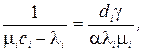
звідки

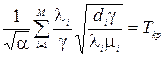. (3.15)

Розв’язавши (3.15) відносно 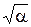маємо

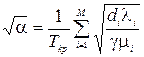. (3.16)

Підставивши (3.16) в розв’язок (3.14) отримаємо остаточний результат

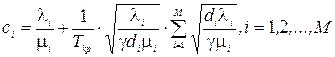(3.17)

При значеннях пропускних спроможностей, які задаються виразом (3.17) час перебування любого об’єкта в мережі не перевищить значення Т_кр, а сукупний капітал, який прийдеться вкласти в мережу буде мінімальним.

Зауваження. В більшості практичних випадків виконується властивість 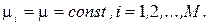Тоді (3.17) прийме вигляд

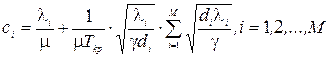(3.18).