Задачі теорії потоків і лінійного програмування
Для подальшого нам знадобляться знання про властивості прямої і двоїстої задачі лінійного програмування. Сформулюємо ці властивості в іншій формі, ніж вони звичайно розглядаються в дослідженні операцій [4, 5]. Наведемо ці властивості без доведення. Пряма задача формулюється таким чином. Потрібно визначити значення змінних 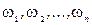 , які задовольняють співвідношенням
, які задовольняють співвідношенням
|
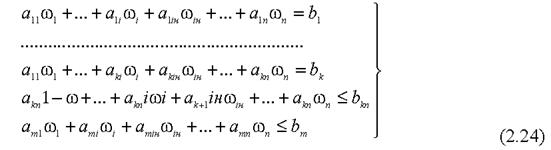
і падають максимуму лінійній формі
|

Для подальшого важливо, що величина 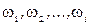 мають любі знаки, а величини
мають любі знаки, а величини 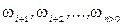 (ці змінні відповідають нерівностям двоїстої задачі).
(ці змінні відповідають нерівностям двоїстої задачі).
Цій прямій задачі ставиться у відповідність двоїста задача. При цьому кожному з обмежень (1.24) ставляться у відповідність двоїсті змінні і 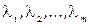 ; для цих змінних складаються обмеження з рівностей і нерівностей
; для цих змінних складаються обмеження з рівностей і нерівностей
(1.26)
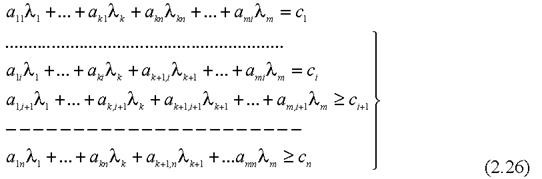
причому змінні 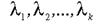 мають довільні знаки, а змінні
мають довільні знаки, а змінні 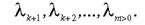
|
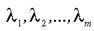 які б задовольняли умовам (1.26) і мінімізували форму
які б задовольняли умовам (1.26) і мінімізували форму

Коефіцієнти в лівій частині (1.26) отримуються транспонуванням матриці системи (1.24).
Вектор 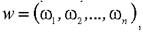 який задовольняє обмеженням основної задачі називається допустимим вектором, а основна задача - допустимою задачею. Допустимий вектор, який максимізує (1.25) називається оптимальним вектором, а задача - оптимальної. Така ж термінологія застосовується для двоїстої задачі.
який задовольняє обмеженням основної задачі називається допустимим вектором, а основна задача - допустимою задачею. Допустимий вектор, який максимізує (1.25) називається оптимальним вектором, а задача - оптимальної. Така ж термінологія застосовується для двоїстої задачі.
Для кожної з цих задач можливі три випадки:
- є оптимальні вектори (а отже і допустимі);
- є допустимі вектори, але немає оптимальних;
- немає допустимих векторів.
|

Припустимо, що основна, а отже і двоїста задача має допустимі вектори.
|
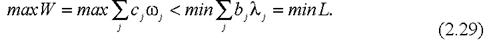
Нехай w і l допустимі вектори, тоді
|

|
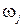 , які приймають значення любого знака, виконуються рівності
, які приймають значення любого знака, виконуються рівності
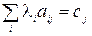 (2.31)
(2.31)
а для невід'ємних змінних 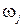 справедливими є нерівності
справедливими є нерівності
|
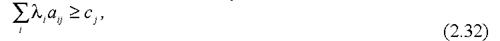
Якщо якась j-та нерівність двоїстої задачі не обертається в точну рівність (є суворою нерівністю), тобто
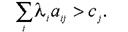
то рівність в формулі (1.30) для допустимих рівнянь можлива тільки при умові, що відповідна j-та змінна основної задачі обертається в нуль, тобто 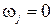 .
.
Ця вимога є необхідною і достатньою. Умовно це можна представити таким чином:
|

Це положення називають другою теоремою двоїстості [4, 5, 29] і формулюють таким чином. Для того, щоб допустимі розв'язки W і l пари двоїстих задач обертали в рівність співвідношення (1.30) тобто були оптимальними, необхідно і достатньо виконання наступної умови: якщо якась з нерівностей системи обмежень однієї задачі не обернулась в точку рівність то відповідна змінна іншої задачі повинна дорівнювати нулю. Аналогічним чином
|

тому що для тих змінних 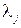 , які мають любий знак, справедливими є рівності
, які мають любий знак, справедливими є рівності
|

Якщо для деякого і в (1.35) виконується знак рівності, то необхідно і достатньо, щоб 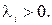
Це положення умовно можна позначити таким чином:
|

Доведено наступні: для того, щоб допустимі розв'язки W і l пари задач обертали (1.34) в рівність (були оптимальними) необхідно і достатньо виконання наступної умови: якщо якась із змінних однієї з двоїстих задач суворо позитивна, то відповідне обмеження іншої (основної) задачі повинно обертатися в рівність. Із порівняння (1.30) і (1.34) виходить, що
|
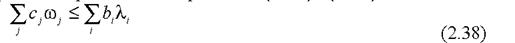
Рівність в (1.37) можлива тоді і тільки тоді, коли виконуються умови (1.33) і (1.36).
Теорему про максимальний потік можна отримати з теореми двоїстості Теорема двоїстості, теорема про максимальний потік і теорема про мінімальне в теорії ігор – це різні формування одного і того ж положення. Розглянемо рівняння, які визначають максимальний потік, і складемо для них двоїсту задачу:
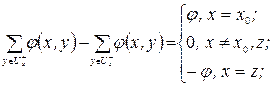 (1.38)
(1.38)
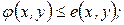 (1.39)
(1.39)
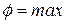 .
.
Неважко переконатися в тому, що матриця коефіцієнтів лівої частини співпадає з матрицею інциденцій.
Співставимо з равенствами (1.38) величини 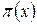 (всього їх N+2, де N – число внутрішніх вершин мережі), а нерівностям (1.39) – величини
(всього їх N+2, де N – число внутрішніх вершин мережі), а нерівностям (1.39) – величини 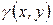
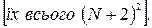 Нагадаємо, що
Нагадаємо, що
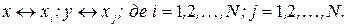
Тоді у відповідності з формальними правилами побудови двоїстої задачі отримаємо:
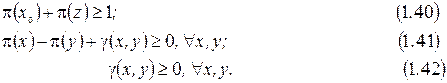
При цих обмеженнях потрібно знайти мінімум лінійної форми
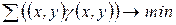 (1.43)
(1.43)
Пояснимо це на прикладі
Приклад 3. неважко переконатися, що для мережі, яка зображена на рис. 5, матриця інциденцій має вигляд:
(1.44)
| (х0, x) | (х0, y) | (х, y) | (y, x) | (х, z) | (y, z) | |
| х0 | ||||||
| х | -1 | -1 | ||||
| у | -1 | -1 | ||||
| z | -1 | -1 |

 Рядки матриці інциденцій відповідають вершинам, стовпчикам, дугам. Якщо дуга виходить з вершини, то на перетині відповідних рядка і стовпчика стоїть +1, якщо входить, то стоїть –1. Коли вершини неінцедентні, тобто не є ні початковою ні кінцевою вершиною дуги, то ставиться нуль. Дамо пояснення до співвідношень (1.40) – (1.44). По-перше, так як лінійна форма основної задачі залежить від величини
Рядки матриці інциденцій відповідають вершинам, стовпчикам, дугам. Якщо дуга виходить з вершини, то на перетині відповідних рядка і стовпчика стоїть +1, якщо входить, то стоїть –1. Коли вершини неінцедентні, тобто не є ні початковою ні кінцевою вершиною дуги, то ставиться нуль. Дамо пояснення до співвідношень (1.40) – (1.44). По-перше, так як лінійна форма основної задачі залежить від величини 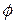 , включимо її в невідомі, перенесли в ліву частину в співвідношеннях (1.38) і добавив в матриці інциденцій відповідний стовпчик
, включимо її в невідомі, перенесли в ліву частину в співвідношеннях (1.38) і добавив в матриці інциденцій відповідний стовпчик
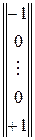
Тоді матриця коефіцієнтів перепишеться в вигляді
| (х0, x1) | (х0, y) | (х, y) | (y, x) | (х, z) | (y, z) | φ | |
| х0 | -1 | ||||||
| х | -1 | -1 | |||||
| у | -1 | -1 | |||||
| z | -1 | -1 | |||||
В останню матрицю добавлено шість рядків, які відповідають нести рівнянням – обмеженням на пропускну спроможність. Випишемо кілька рівнянь, які відповідають рівнянням (1.45) в розвернутому вигляді.
Для х = х0 друга сума в (1.38) не дає ні одного члена;
Для х ≠ х0, z друга сума дає два члени. Тоді (1.38) буде мати вигляд:
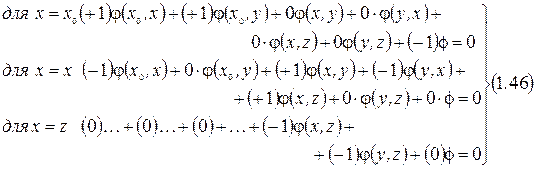
Якщо транспортувати матрицю (1.45) і врахувати, що 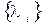 відповідає першому рівнянню в (1.46), а
відповідає першому рівнянню в (1.46), а 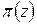 – останньому, то отримаємо рівняння (1.40).
– останньому, то отримаємо рівняння (1.40).
Одиниця в правій частині (1.40) стоїть тому, що відповідний коефіцієнт лінійної форми дорівнює одиниці.
Можна показати, що якщо 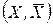 – мінімальний розріз, який відділяє х0 від z, то оптимальний розв’язок двоїстої задачі дається формулами
– мінімальний розріз, який відділяє х0 від z, то оптимальний розв’язок двоїстої задачі дається формулами
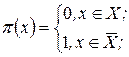 (1.47)
(1.47)
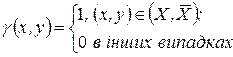 (1.48)
(1.48)
Цікаво відмітити, що розв’язки (1.47) і (1.48) дають: розв’язок двоїстої задачі – мінімальний розріз, розв’язок прямої задачі – максимальний потік.
Дата добавления: 2016-07-22; просмотров: 1998;











