Графічний метод розв’язування задач лінійного програмування

Для кращого розуміння основних властивостей задач лінійного програмування використаємо їх геометричне зображення. Введемо визначення опуклих множин, які характерні для задач лінійного програмування.

Множина D в n-мірному евклідовому просторі називається опуклою множиною, якщо для будь-яких двох точок цієї множини 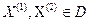точки X = 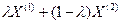належать множині D для всіх значень X, які належать відрізку [0; 1]. Геометрично це означає, що якщо дві точки належать множині D то й відрізок прямої, що їх з’єднує, також належить до множини D. Прикладами опуклих множин на площині є відрізок, пряма, круг, півплощина, квадрат і т.д.

Розглянемо основні властивості розв’язків задач лінійного програмування.

Вектор Х=(х₁, х₂, ... , х_п), координати якого задовольняють систему обмежень (3.2) і (3.3), називають допустимим розв’язком (планом) задачі. Сукупність допустимих розв’язків задачі утворює область допустимих розв’язків.

Опорним планом задачі лінійного програмування називається план, що утворений координатами вершин многогранника планів задачі. Отже, опорний план – це план, який задовольняє не менш ніж п лінійно незалежних обмежень (3.2) та обмеження (3.3) щодо знака у вигляді строгих рівностей.

Опорний план називається невиродженим, якщо він є вершиною многогранника планів задачі, що утворений перетином п гіперплощин, тобто задовольняє п лінійно незалежних обмежень – строгих рівностей. В протилежному випадку опорний план є виродженим.

Якщо задача лінійного програмування має розв’язок і серед її планів є опорні, то хоча б один з них буде оптимальним. Сукупність усіх розв’язків задачі лінійного програмування є багатогранною опуклою множиною, яку називають многогранником розв’язків. Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин многогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього многогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Розглянемо алгоритм графічного методурозв’язування задач лінійного програмування. Слід зауважити, що окреслений метод використовується для розв’язування певного класу задач лінійного програмування, зокрема задач, число невідомих яких не перевищує 3. Хоча вже в трьохвимірному просторі важко побудувати многогранник допустимих розв’язків, а задачу лінійного програмування, яка містить більше трьох змінних графічно зобразити практично неможливо. Тому найчастіше графічним методом розв’язують задачі лінійного програмування, які містять дві невідомі і записані в другій стандартній формі (з обмеженнями-нерівностями).

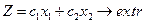
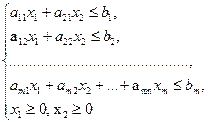
Розглянемо основні етапи знаходження розв’язку задач ЛП графічним методом:

1) На координатній площині Х₁0Х₂ будуємо граничні прямі, які відповідають системі обмежень задачі:

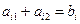, i = .

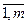2) Визначаємо півплощини, які є розв’язками нерівностей. Для цього беремо координата точки з довільної півплощини і підставляємо в нерівність. Якщо нерівність справджується, то півплощина розв’язків направлена в сторону вибраної точки, якщо ж не справджується, то в протилежну сторону.

3) Знаходимо область, де перетинаються всі півплощини розв’язків – многокутник розв’язків. Якщо перетин – непорожня множина, то переходимо до наступного етапу. В протилежному випадку робимо висновок, що задача не має розв’язку.

4) Будуємо вектор нормалі 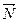, початок якого знаходиться в точці (0,0), а друга координата - в точці (с₁,с₂) (коефіцієнти при невідомих в цільовій функції). Вектор нормалі вказує напрямок зростання функції.

5) Перпендикулярно до вектора нормалі будуємо лінію рівнів с₁х₁ + с₂х₂ = const. Для зручності знаходження оптимальних точок лінію рівнів будуємо так, щоб вона мала спільні точки з многокутником розв’язків (перетинала многокутник розв’язків).

6)Визначаємо оптимальні точки. Для цього лінію рівнів паралельно переносимо в напрямку вектора нормалі. Остання вершина многокутника, яку перетне лінія рівнів, буде точкою максимуму. Потім лінію рівнів паралельно переносимо в напрямку, протилежному напрямку вектора нормалі. Остання вершина многокутника розв’язків, яку перетне лінія рівнів в цьому випадку, є точкою мінімуму.

7)Знаходимо найбільше та найменше значення функції. Для цього підставимо координати оптимальних точок, знайдених шляхом розв’язування систем рівнянь граничних прямих (перетином яких є оптимальна точка), в цільову функцію.