Основні поняття та означення теорії потоків

Як говорилося вище, теорія потоків має справу з класом графів, які називаються транспортними мережами або просто мережами.

Скінчений граф (Х, Т) без петель називається сіткою, якщо кожній дузі 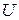співставлень у відповідальність ціле число 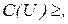яке називається пропускною спроможністю дуги. Цьому графу властиві наступні властивості:

1) існує одна і тільки одна вершина х₀, з якої дуги виходять, але ні одна не входить. Ця вершина називається входом або джерелом сітки;

2) існує одна і тільки одна вершина графа Z, в яку входять дуги, але ні одна дуга не виходить. Ця вершина називається виходом, або стоком сітки (мережі).

Для сіток вводять поняття потоку. Хай 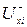множина дуг, які входять в вершину х_і, а 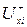– множина дуг, які виходять з вершини х_і. Функція 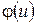, яка визначена на множині дуг сітки n і приймає цілочисельні позитивні значення, являє собою потік даної транспортної сітки, якщо

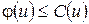; (1.1)

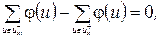
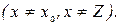(1.2)

Перша умова означає, що потік дуги не може перевищувати її пропускну спроможність. Друга умова стверджує, що сумарний потік дуг, які входять в вершину, дорівнює сумарному потоку, який з вершини виходить (за виключенням точок входу і виходу). Інколи остання залежність називається умовою збереження потоку, тому що вона стверджує, що в любій проміжній точці потік не створюється і не щезає.

Ясно, що транспортні мережі, типа мережі автомобільних чи залізничних мереж, мережі ліній зв’язку (телеграфних, телевізійних, телефонних), задовольняють цим умовам і володіють потоком. Дуги можна інтерпретувати, як шляхи сполучення; пропускна спроможність дуги в цьому випадку можна сприймати як кількість одиниць потоку, який може бути пропущений по конкретній дузі в одиницю часу. В цьому випадку значення потоку на дузі 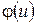являє собою кількість товарів, які дійсно перевозяться по дузі в одиницю часу.

Введемо поняття сумарного на кінцевих дугах сітки, яке відрізняється від поняття потоку на дузі 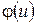. З (1.2) виходить, що сума потоків, які виходять з початкової вершини х₀ дорівнює сумі потоків, які входять в кінцеву вершину Z

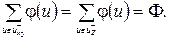(1.3)

Коли говорять, що на сітці заданий потік, то це означає, що задані дугові потоки 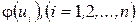, де n – кількість дуг в графі сітки.

Припустимо, що множина всіх вершин даної мережі розбито на дві взаємно доповнюючих множини 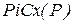, причому перша підмножина містить в собі вхід мережі 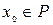, а друге – вихід мережі 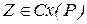, тобто всі вершини мережі, які не ввійшли в підмножину Р, повинні міститися в підмножині .

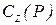В цьому випадку говорять, що в сітці проведений розріз.

Множина дуг 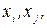де 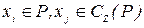, називається розрізом. Сума пропускних спроможностей дуг розрізу називається величиною розрізу і позначається Г або Г[Y, C(Y)]. В останньому позначенні вказують взаємні доповнюючи підмножини, які визначають розріз. Як правило, зі зміною розрізу змінюються і його значення.

В загальному випадку величини потоку на кінцевих дугах ніколи не перевищує величину розрізу

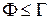(1.4)

Доведемо це співвідношення (хоча це логічно ясно). З формули (1.3) виходить, що

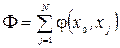(1.5)

Тут через 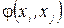позначається потік дуги, яка з’єднує вершини 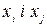, причому вважається, що

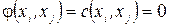(1.6)

якщо не існує дуги .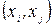

Загальна кількість вершин в мережі, не рахуючи входу і виходу, дорівнює N. Додамо до обох частин рівності (1.5) величину

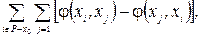(1.7)

де через Р-х₀ позначена одна з підмножин розрізу без початкової точки; 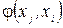– потік на дузі .

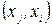При цьому вважається, що потік тече в обидва боки, тобто ці вершини з’єднують пряма і зворотна дуга.

Величина (1.7) у відповідності до співвідношення (1.2) дорівнює нулю. В результаті отримаємо:

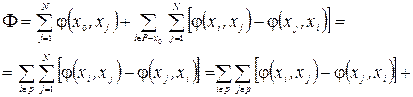
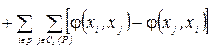(1.8)

Тому що при фіксованому 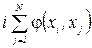дорівнює сумарному потоку, який виходить з вершини і, а 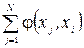– сумарному потоку, який входить в вершину і.

Перший доданок в останній частині (1.8) дорівнює нулю, тому що всі його доданки взаємно знищуються. Отже,

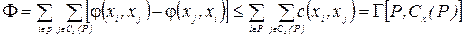(1.9)

Тут використана на умові, згідно якої, значення потоку на дузі не перевищує її пропускної спроможності

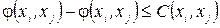. (1.10)

В зв’язку з тим, що реальний потік не може бути від’ємним, то за позитивний напрямок приймають напрямок більшого потоку. Вираз (1.10) означає, що дві дуги в протилежних напрямках між двома вершинами можна замінити однією, потік в якій визначається за допомогою (1.10).