Двоїстість у задачах лінійного програмування: правила побудови двоїстих задач та їх основні класи

Кожній задачі лінійного програмування відповідає двоїста, яка формується за допомогою певних правил безпосередньо з умов прямої задачі. Нехай задача лінійного програмування має вигляд:

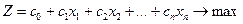(4.1)

за умов

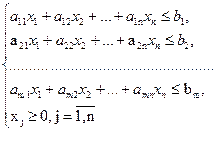(4.2)

1. Кожному основному обмеженню початкової задачі ставимо у відповідність двоїсту змінну: першому обмеженню – у₁, другому – у₂, ..., m-му – у_m. Кількість невідомих двоїстої задачі дорівнює кількості основних обмежень прямої задачі лінійного програмування:

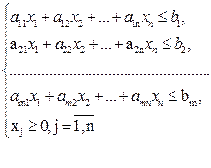
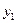
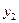
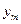
2. Якщо цільова функція початкової задачі досліджується на максимум, то двоїстої – на мінімум, і навпаки.

3. Щоб записати цільову функцію двоїстої задачі, потрібно праві частини основних обмежень початкової задачі перемножити на двоїсті змінні, що відповідають кожному з цих обмежень і додати. Отже, коефіцієнтами при невідомих в цільовій функції двоїстої задачі є праві частини основних обмежень прямої задачі. Вільний член цільової функції прямої задачі переноситься без змін в цільову функцію двоїстої:

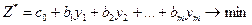
4. Обмеження двоїстої задачі формуємо таким чином: коефіцієнти при невідомій кожного основного обмеження системи (4.2) множимо на відповідні двоїсті змінні і додаємо. В результаті отримуємо ліві частини обмежень двоїстої задачі:

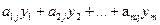. Правими частинами обмежень двоїстої задачі є коефіцієнти при невідомій 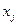в цільовій функції початкової задачі ( 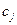). Отже, кількість змінних прямої задачі дорівнює кількості основних обмежень двоїстої.

5. Враховуючи, що в основних обмеженнях початкової задачі знак нерівності « 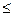», то в обмеженнях двоїстої задачі знак нерівності буде « ».

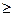6. Матриця

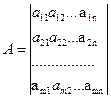
що складається із коефіцієнтів при невідомих в системі обмежень прямої задачі, і матриця коефіцієнтів при невідомих системи обмежень двоїстої задачі лінійного програмування утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків – рядками.

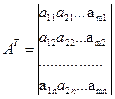
В результаті отримаємо двоїсту задачу:

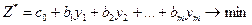
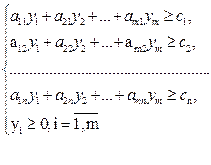
Двоїсті пари задач лінійного програмування бувають симетричні та несиметричні.

У симетричних задачах обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень.

У несиметричних задачах обмеження прямої задачі можуть бути записані у вигляді рівнянь, а двоїстої - лише у вигляді нерівностей. В цьому випадку відповідні змінні двоїстої задачі можуть приймати будь-яке значення, необмежене знаком.