Стверджується, що кінцева вершина
z Î X. (1.20)
|

Який на рис. 4 має ту властивість, що для прямих дуг цієї мережі.
|

а для зворотних буде
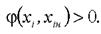
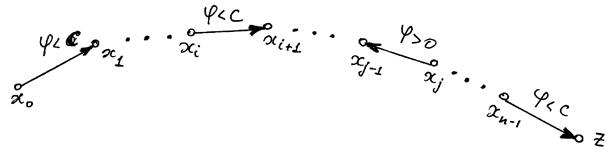
Рис. 4. Пояснення до теореми про максимальний потік
Позначимо через e1 мінімум різниці 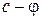 який береться по всім прямим дугам цього шляху, а через e2 – мінімум по всім зворотнім дугам. Введемо величину
який береться по всім прямим дугам цього шляху, а через e2 – мінімум по всім зворотнім дугам. Введемо величину 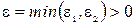 . Змінимо потік j, збільшивши його на e на всіх прямих дугах шляху, тобто
. Змінимо потік j, збільшивши його на e на всіх прямих дугах шляху, тобто  і зменшивши його на цю величину на всіх зворотних дугах, тобто
і зменшивши його на цю величину на всіх зворотних дугах, тобто 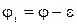 .
.
В цьому випадку величина сумарного потоку на кінцевих дугах мережі, яка була Ф складає
|
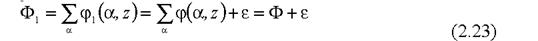
Але (1.23) суперечить тій умові, що потік в мережі j є максимальним. Таким чином (1.20) доведено, отже доведена теорема про максимальний потік.
З цього факту випливає важливий наслідок:
Потік j є максимальним в тому і тільки в тому випадку, якщо нема ні одного шляху, який збільшує його.
Цей наслідок дає ефективний засіб визначення максимального потоку. Для того, щоб потік зробити максимальним, необхідно наситити всі дуги розрізу 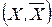 .
.
Дата добавления: 2016-07-22; просмотров: 2153;











