Характеризация бесконечно-удалённой точки.
Когда мы вычисляем предел в точке  , он может быть конечным, бесконечным либо не существовать. Аналогично этому, подобные ситуации могут быть и при вычислении предела
, он может быть конечным, бесконечным либо не существовать. Аналогично этому, подобные ситуации могут быть и при вычислении предела  при
при 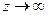 . Бесконечность не является точкой в плоскости, тем не менее, тип такого объекта как «бесконечно-удалённая точка» можно тоже классифицировать как и типы особых точек, с помощью предела.
. Бесконечность не является точкой в плоскости, тем не менее, тип такого объекта как «бесконечно-удалённая точка» можно тоже классифицировать как и типы особых точек, с помощью предела.
Существует геометрическая модель, в которой бесконечно-удалённая точка присутствует на равных с другими точками. Поместим сферу над плоскостью в начало координат. Если от верхней точки S провести любую наклонную прямую, то она 1 раз пересечётся со сферой и 1 раз с плоскостью. Таким образом, каждой точке комплексной плоскости можно однозначно поставить в соответствие точку на сфере. При этом единственная точка, для которой нет образа на плоскости - это точка S. Она соответствует горизонтальной касательной, и можно поставить ей в соответствие «бесконечно удалённую точку».
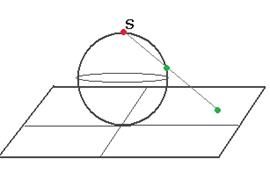
Если на плоскости точка устремится к 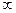 , то её образ на сфере устремится к точке S.
, то её образ на сфере устремится к точке S.
Классификация 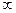 как особой точки происходит аналогично, как и было для точки
как особой точки происходит аналогично, как и было для точки  :
:
| Название | Устранимая особая точка | Полюс | Существенно-особая точка |
| При каком условии | 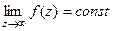
| 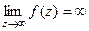
| 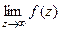 не существует
не существует
|
| Пример |  = = 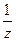
|  = = 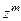
|  = = 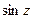
|
Только в данном случае наоборот, полюс если степень m в числителе, а не в знаменателе. Например, для 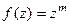 полюс порядка m.
полюс порядка m.
В задачах можно делать замену 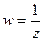 и таким образом сводить изучение
и таким образом сводить изучение 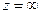 к изучению поведения функции в точке
к изучению поведения функции в точке 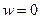 .
.
Пример. Определить тип точки 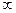 для
для 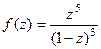 .
.
Решение.Сделаем замену 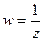 , т.е. После этого функция изменит вид так:
, т.е. После этого функция изменит вид так: 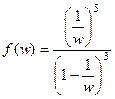 =
= 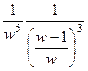 =
= 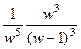 .
.
Попутно заметим, что 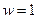 а значит и
а значит и 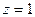 - полюс 3-го порядка.
- полюс 3-го порядка.
Для точки 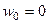 , соответствующей
, соответствующей 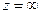 , видим нуль 3-го порядка в числителе и 5-го порядка в знаменателе. Сократив дробь, можно получить
, видим нуль 3-го порядка в числителе и 5-го порядка в знаменателе. Сократив дробь, можно получить 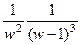 . Тогда видно, что
. Тогда видно, что 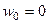 полюс 2-го порядка, а значит,
полюс 2-го порядка, а значит, 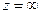 полюс 2-го порядка.
полюс 2-го порядка.
Пример. Определить тип точки 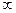 для
для 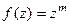 .
.
Решение.Сделаем замену 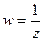 , т.е. После этого функция станет
, т.е. После этого функция станет 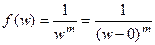 , то есть
, то есть 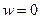 полюс порядка m, значит
полюс порядка m, значит 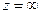 полюс порядка m.
полюс порядка m.
Пример. Определить тип точки 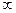 для
для 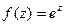 .
.
Решение.Сделаем замену 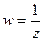 , т.е. После этого
, т.е. После этого 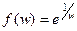 .
.
Если устремить 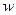 к 0 со стороны положительной полуоси, то получается
к 0 со стороны положительной полуоси, то получается 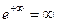 . Если со стороны отрицательной полуоси, то
. Если со стороны отрицательной полуоси, то 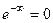 . А если со стороны мнимой оси, то предел вообще не существует: при
. А если со стороны мнимой оси, то предел вообще не существует: при 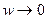 ,
, 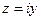 , и при этом
, и при этом 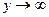 , при этом
, при этом 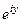 =
= 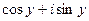 , т.е. при
, т.е. при 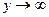 не существует предел ни действительной, ни мнимой части. Итак, приближаясь к (0,0) на плоскости с разных сторон, получаем разные результаты, а при приближении по некоторым траекториям предел даже не существует.
не существует предел ни действительной, ни мнимой части. Итак, приближаясь к (0,0) на плоскости с разных сторон, получаем разные результаты, а при приближении по некоторым траекториям предел даже не существует.
Вывод: предел в точке 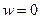 не существует,
не существует, 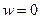 а значит
а значит 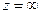 это существенно-особая точка.
это существенно-особая точка.
Вычеты.
Определение.Пусть 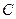 замкнутый контур, внутри него точка
замкнутый контур, внутри него точка  , на самом контуре и внутри него нет особых точек, кроме
, на самом контуре и внутри него нет особых точек, кроме  . Тогда интеграл
. Тогда интеграл 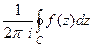 называется вычетом функции
называется вычетом функции  в точке
в точке  и обозначается
и обозначается 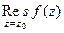 .
.
Дата добавления: 2020-10-14; просмотров: 559;











