Особые точки и вычеты

Нули.

Определение.Точка называется нулём функции , если .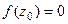

Мы сначала изучим нули функции, для того, чтобы затем изучить более подробно типы точек разрыва. Если является нулём для то в этой же точке предел 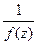равен .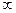

Вспомним, что в 1 семестре было ещё название «бесконечно-малая» и «бесконечно-большая» функция в точке. Бесконечно-малые могли быть разных порядков. Есть и здесь аналогичное более подробное определение, различающее порядки бесконечно малых:

Определение.Точка называется нулём порядка m функции , если 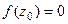и функция представима в ви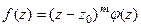де , где .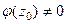

Особые точки.

Определение.Точка называется правильной точкой функции , если является аналитической в , и особой точкой, если она не является аналитической в .

Определение.Точка называется изолированной особой точкой, если в некоторой её окрестности нет других особых точек.

Бывают и не изолированные особые точки, например, для функции 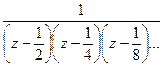последовательность особых точек сходится к 0, и 0 не является изолированной особой точкой.

Существует такая классификация особых точек в зависимости от предела .

Название	Устранимая особая точка	Полюс	Существенно-особая точка
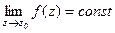
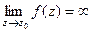
При каком условии			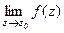не существует
Пример ( )	=	=	=

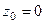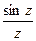
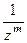
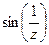
Лемма.Точка является нулём функции 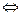она является полюсом функции .

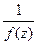Док-во очевидно: является нулём функции 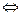функция представима в виде 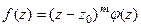, причём

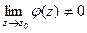. Это эквивалентно тому, что =

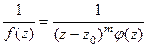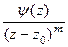, где 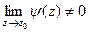, а предел знаменателя равен 0. Это означает, что .

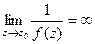В связи с этим, естественным образом возникает определение полюса порядка 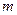: точка называется полюсом порядка m для функции , если для функции 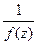она является нулём порядка m.

Замечание.Нуль и полюс функции соответствуют понятиям «бесконечно малая» и «бесконечно большая» функция в точке (из 1 семестра). Если даже бесконечно малая функция не была степенная, то выделяли главную часть вида 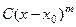. То есть, другими словами, как раз и находили, что точка является нулём порядка m.

Пример. Указать тип всех особых точек для функции:

.

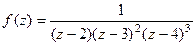Решение.В знаменателе нули 1-го, 2-го и 3-го порядка, а именно, точки 2,3 и 4. Тогда для : 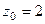полюс 1-го порядка,

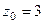полюс 2-го порядка, 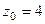полюс 3-го порядка.

Теорема.Если 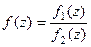, причём точка является нулём порядка m для функции 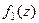, и нулём порядка n для функции 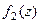, то при 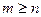точка устранимая или правильная точка, а при 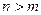полюс порядка для функции .

Доказательство. Если - нуль порядка m и n соответственно для числителя и знаменателя, то 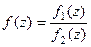= = 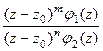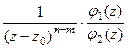где 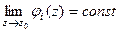для каждой из двух функций. Тогда можно обозначить 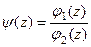и в итоге 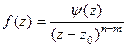, это и означает, что полюс порядка .

Пример. Определить тип особой точки 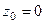для функции .

Решение.Представим функцию в числителе в виде разложения в ряд Тейлора.

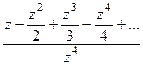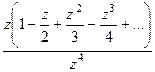= = в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка 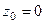полюс 3 порядка.

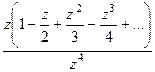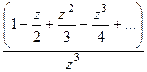= = . В числителе после сокращения осталась функция, имеющая ненулевой предел.