Движение материальной точки. Метод кинетостатики

Иметь представление о свободных и несвободных материаль­ных точках, о силах инерции, об использовании силы инерции для решения технических задач.

Знать формулы для расчета силы инерции при поступатель­ном и вращательном движениях, знать принцип Даламбера и уметь определять параметры движения с использованием законов динамики и метода кинетостатики.

Свободная и несвободная точки

Материальная точка, движение которой в пространстве не огра­ничено какими-нибудь связями, называется свободной. Задачи реша­ются с помощью основного закона динамики.

Материальные точки, движение которых ограничено связями, называются несвободными.

Для несвободных точек необходимо определять реакции связей. Эти точки движутся под действием активных сил и ограничиваю­щих движение реакций связей (пассивных сил).

Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождаемое от связей).

Сила инерции

Инертность — способность сохранять свое состояние неизмен­ным, это внутреннее свойство всех материальных тел.

Сила инерции — сила, возникающая при разгоне или торможе­нии тела (материальной точки) и направленная в обратную сторо­ну от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом.

Рассчитано, что сила инерции равна Fин =‌ ‌‌/‌ma/.

Тема 1.13. Движение материальной точки 101

Таким образом, силы, действующие на материальные точки m1 и m2 (рис. 14.1), при разгоне платформы соответственно равны

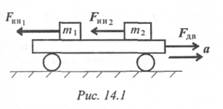
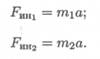Разгоняющееся тело (плат­форма с массой т (рис. 14.1)) силу инерции не воспринимает, иначе разгон платформы вооб­ще был бы невозможен. При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нор­мального а_п и касательного at (рис. 14.2).

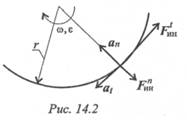
Поэтому при рассмотрении кри­волинейного движения могут воз­никнуть две составляющие силы инерции: нормальная и касательная

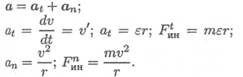
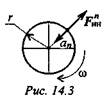
При равномерном движении по дуге всегда возникает нормаль­ное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги (рис. 14.3).

ω = const

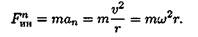
Принцип кинетостатики (принцип Даламбера)

Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции приложены к телам, связанным с разго­няющимся телом (к связям).

102 Лекция 14

Даламбер предложил условно прикладывать силу инерции к ак­тивно разгоняющемуся телу. Тогда система сил, приложенных к ма­териальной точке, становится уравновешенной, и можно при реше­нии задач динамики использовать уравнения статики.

Принцип Даламбера:

Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равнове­сии:

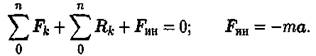
Работа и мощность

Иметь представление о работе силы при прямолинейном и криволинейном перемещениях, о мощности полезной и затрачен­ной, о коэффициенте полезного действия.

Знать зависимости для определения силы трения, формулы для расчета работы и мощности при поступательном и враща­тельном движениях.

Уметь рассчитывать работу и мощность с учетом потерь на трение и сил инерции.

Работа

Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы».

Работа служит мерой действия силы, работа — скалярная ве­личина.