Динамика материальной точки. Законы Ньютона

1 Динамика (от греческого dynamis – сила) изучает движение тел в связи с причинами, определяющими характер движения. К кинематическим величинам - координатам, скорости и ускорению - здесь добавляются ещё динамические - масса тел как мера их инертности и сила – как мера взаимодействия тел.

Материальной точкой называется модель, обладающая одним свойством - массой. Модель материальной точки применима к телам, двигающимся поступательно, или когда размеры тел малы по сравнению с пространственными характеристиками их движения.

2. Законы Ньютона, 1687 г.

Первый закон. Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного прямолинейного движения, пока и поскольку не понуждается другими телами изменить это состояние.

Первый закон называют ещё законом инерции. Его содержание было открыто Галилеем, а его роль в механических явлениях установлена Ньютоном.

Явление сохранения состояния покоя или равномерного прямолинейного движения тел при отсутствии внешних сил называют инерцией.

Второй закон. Скорость изменения импульса тела пропорциональна действующей на тело силе и направлена вдоль той прямой, по которой эта сила действует, = kF. (7.1)

Здесь p = mv - импульс тела, k - коэффициент пропорциональности.

Третий закон. Действию есть равное и противоположное противодействие. Иначе, силы, с которыми две точки действуют друг на друга, равны по величине и направлены вдоль прямой, проходящей через эти точки, 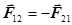. (7.2)

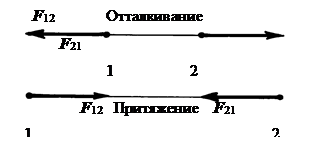Первая цифра индекса означает тело, на которое действует сила, вторая цифра - тело, со стороны которого действует сила, (рис.19).

Хотя законы Ньютона были открыты не в результате целенаправленно поставленных экспериментов, они, тем не менее, есть обобщение опытных фактов. Это экспериментальные законы, они первичны, к ним нельзя придти путём логических рассуждений, отталкиваясь от каких-то других законов.

3. Сила есть количественная мера взаимодействия тел. Это векторная величина, обозначается обычно символами F, f. Единица силы в СИ - ньютон (Н). Она выбирается так, чтобы коэффициент пропорциональности во втором законе Ньютона обратился в единицу. Итак, второй закон динамики (7.1) в СИ имеет вид: 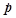= F, или . (7.3)

Если на тело действует несколько сил, то каждая из сил не зависит от других сил и не влияет на них. Это так называемый принцип независимости действия сил. Равнодействующая нескольких сил находится как сумма векторов.

Силы могут проявляться статически в деформации тел и динамически в ускорении движения тел. При статическом проявлении сила измеряется по величине упругой деформации по закону Гука. Эталонная сила: F₀. Измеряемая сила: F.

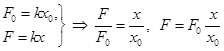. (7.4)

При динамическом проявлении сила измеряется по величине ускорения тела.

. (7.5)

4. Масса тел есть мера их инертности. В классической механике, когда скорости движения тел много меньше скорости света, v << c, масса есть скаляр, всегда положительное число, не изменяющееся при любых взаимодействиях тел при условии сохранения их целостности. Поэтому в Механике малых скоростей справедлив закон сохранения массы.

Поскольку m > 0, то масса нескольких тел равна сумме их масс. Говорят, масса обладает свойством аддитивности.

Измерение масс можно сделать сравнением ускорений тел под действием одной и той же силы. Эталонная масса: m₀,. Измеряемая масса: m.

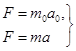Þ ma = m₀a₀, m = m₀ 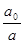. (7.6)

Единица массы в СИ – килограмм (кг).

5. Силы в природе. В настоящее время физика выделяет в природе четыре типа фундаментальных, то есть не сводимых к другим, взаимодействий. Это - гравитационное, электромагнитное, сильное и слабое.

а. Гравитационное, 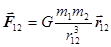– сила тяготения. (7.7)

б. Электромагнитное, 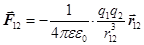(7.8)

– кулоновская сила взаимодействия точечных электрических зарядов.

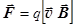– сила Лоренца действия магнитного поля на движущийся заряд. (7.9)

F_x = - kx – сила упругой деформации (закон Гука). (7.10)

F = mN – сила сухого трения (закон Кулона-Амонтона).(7.11)

Сильное и слабое взаимодействие проявляется между элементарными частицами в явлениях, для которых модели классической механики неприменимы. Поэтому при описании этих взаимодействий не применяется практически понятие силы.

6. Уравнение движения. Преобразуем форму 2-го закона Ньютона (или часто говорят - второго закона динамики): , или 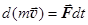. (7.12)

Произведение силы 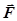на время её действия dt называют импульсом силы. Поэтому второй закон Ньютона можно сформулировать ещё так: изменение импульса тела d(m 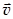) пропорционально импульсу действующей на это тело силы 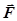dt. Так как при малых скоростях m = const, то . Отсюда , где 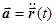. (7.13)

Формулу второго закона Ньютона, записанную через производную импульса материальной точки или его координат, называют уравнением движения материальной точки: 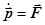, или . (7.14)

В правой части символом F обозначена равнодействующая всех сил, приложенных к материальной точке, т.е. .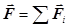

Часто уравнение движения записывают в проекциях на оси координат.

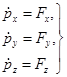или 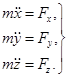(7.15)

Наиболее часто в задачах механики известны силы, действующие на тело. Чтобы описать движение тела, нужно найти его скорость и координаты в любой момент времени. А для этого нужно интегрировать уравнение движения.

Поиск кинематических характеристик – координат и скоростей – материальной точки по известным силам, действующим на неё, называют второй задачей динамики. Она решается интегрированием уравнения движения.

Бывают ситуации, когда известен кинематический закон движения точки, то есть, известны её координаты в любой момент времени, и нужно найти силы, действующие на точку. Это, так называемая, первая задача динамики. Она решается дифференцированием кинематического закона движения.