Интегральная формула Коши
Заметим, что в примере 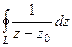 =
= 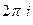 в прошлой лекции
в прошлой лекции
результат получился не зависящим от радиуса 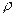 . То есть при уменьшении или увеличении окружности ничего не изменится, если та же самая точка разрыва остаётся внутри, а замкнутый контур стягивается к ней, оставляя снаружи область аналитичности. Этот факт докажем в общем случае.
. То есть при уменьшении или увеличении окружности ничего не изменится, если та же самая точка разрыва остаётся внутри, а замкнутый контур стягивается к ней, оставляя снаружи область аналитичности. Этот факт докажем в общем случае.
Теорема 1. (Интегральная теорема Коши).
Пусть 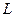 некоторый замкнутый контур,
некоторый замкнутый контур, 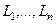 - n замкнутых непересекающихся контуров, лежащих внутри
- n замкнутых непересекающихся контуров, лежащих внутри 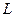 . Функция
. Функция  является аналитической на всех этих контурах, а также внутри
является аналитической на всех этих контурах, а также внутри 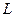 , но вне
, но вне 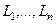 . Тогда
. Тогда 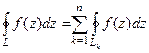 .
.
Доказательство.
Для того, чтобы лучше понять идею доказательства, рассмотрим сначала ситуацию, когда внутри 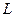 расположен один контур
расположен один контур 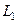 , то есть область аналитичности - кольцо. Можно взять какую-либо пару точек
, то есть область аналитичности - кольцо. Можно взять какую-либо пару точек 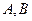 на
на 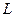 и
и 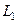 соответственно (чтобы точкибыли максимально близко напротив друг друга) и соединить их отрезком. Тогда для комбинированого контура, состоящего из 4 частей:
соответственно (чтобы точкибыли максимально близко напротив друг друга) и соединить их отрезком. Тогда для комбинированого контура, состоящего из 4 частей: 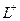 ,
, 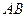 ,
, 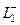 ,
, 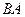 внутренняя область, похожая на кольцо с разрезом, это область аналитичности. Мы один раз обходим этот контур, двигаясь по внешнему против часовой стрелки, поэтому и обозначено
внутренняя область, похожая на кольцо с разрезом, это область аналитичности. Мы один раз обходим этот контур, двигаясь по внешнему против часовой стрелки, поэтому и обозначено 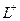 , затем переходя на внутренний контур по
, затем переходя на внутренний контур по 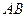 , затем двигаясь по внутреннему в противоположном направлении (
, затем двигаясь по внутреннему в противоположном направлении ( 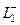 ), и возвращаясь по
), и возвращаясь по 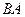 снова на внешний контур. Чертёж:
снова на внешний контур. Чертёж:
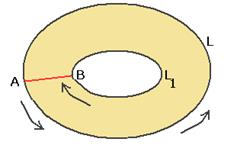
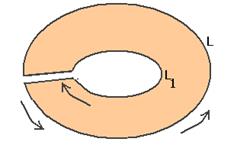
Но если комбинированный контур окружает область аналитичности, то интеграл по нему равен 0. Внутренняя область при этом фактически становится внешней (для нового контура, который с разрезом, на правом чертеже).
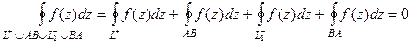 .
.
При этом интегралы по 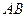 и
и 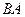 и так взаимно уничтожаются, поэтому
и так взаимно уничтожаются, поэтому 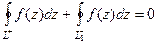 . Но если сменить направление движение по внутреннему контуру
. Но если сменить направление движение по внутреннему контуру 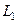 , то интеграл по нему сменил бы знак, тогда:
, то интеграл по нему сменил бы знак, тогда: 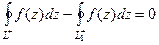
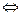
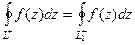 .
.
Таким образом, интегралы по 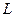 и
и 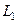 одинаковы, то есть можно без изменения результата уменьшить область, стянув её к точке разрыва, оставив снаружи какую-то часть области аналитичности.
одинаковы, то есть можно без изменения результата уменьшить область, стянув её к точке разрыва, оставив снаружи какую-то часть области аналитичности.
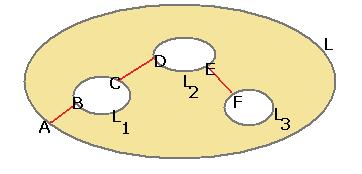
Если внутри 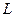 несколько контуров, внутри которых нарушена аналитичности или даже существование функции, то применяется похожая схема рассуждений, только надо поочерёдно соединить отрезком
несколько контуров, внутри которых нарушена аналитичности или даже существование функции, то применяется похожая схема рассуждений, только надо поочерёдно соединить отрезком 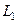 с
с 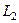 , затем
, затем 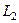 с
с 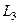 и так далее, до номера n.
и так далее, до номера n.
Получится 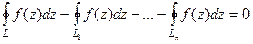 , откуда
, откуда
следует 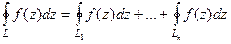 .
.
Теорема 2. (Интегральная формула Коши).
Пусть  является аналитической на контуре
является аналитической на контуре 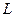 и внутри него, точка
и внутри него, точка 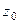 лежит внутри
лежит внутри 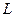 . Тогда
. Тогда 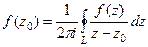 .
.
Доказательство.
В рассмотренном примере в конце прошлой лекции мы вычислили 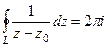 , то есть верно
, то есть верно 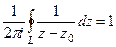 . Но мы можем домножить это равенство на любую комплексную константу, и тогда:
. Но мы можем домножить это равенство на любую комплексную константу, и тогда: 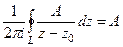 . Впрочем, тогда это же верно и для константы
. Впрочем, тогда это же верно и для константы 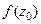 : получаем
: получаем 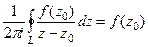 . Мы получили выражение, очень похожее на то, которое надо доказать, но ещё не то: ведь здесь в числителе константа, а не функция. Вот если мы теперь ещё и докажем, что
. Мы получили выражение, очень похожее на то, которое надо доказать, но ещё не то: ведь здесь в числителе константа, а не функция. Вот если мы теперь ещё и докажем, что 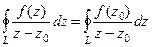 , или то же самое, что
, или то же самое, что 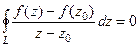 , то требуемое утверждение будет верно.
, то требуемое утверждение будет верно.
Рассмотрим функцию 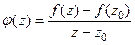 . Это функция, которая участвует в определении производной, ведь
. Это функция, которая участвует в определении производной, ведь 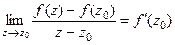 .
.
Таким образом, 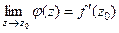 , то есть
, то есть 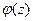 имеет конечный предел в точке
имеет конечный предел в точке 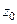 , а это значит, что она ограничена в окрестности этой точки,
, а это значит, что она ограничена в окрестности этой точки, 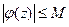 . По теореме 1 (интегральная теорема Коши), интеграл по
. По теореме 1 (интегральная теорема Коши), интеграл по 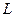 можно заменить на интеграл по любой малой окружности
можно заменить на интеграл по любой малой окружности 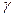 радиуса
радиуса 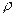 , лежащей внутри
, лежащей внутри 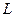 , результат при этом не изменится. Тогда
, результат при этом не изменится. Тогда 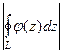 =
= 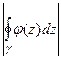
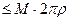 , где
, где 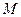 - максимальное значение модуля функции,
- максимальное значение модуля функции, 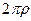 - длина кривой, по которой происходит интегрирование. Но ведь по теореме 1 это должно быть верно для какого угодно малого
- длина кривой, по которой происходит интегрирование. Но ведь по теореме 1 это должно быть верно для какого угодно малого 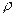 . То есть
. То есть 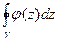 меньше или равен любой бесконечно-малой величины. Тогда этот интеграл равен 0. То есть
меньше или равен любой бесконечно-малой величины. Тогда этот интеграл равен 0. То есть 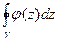 =
= 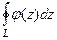 =
= 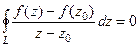 . Значит,
. Значит, 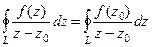 , а тогда:
, а тогда:
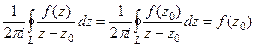 , т.е.
, т.е. 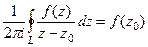 доказано в итоге.
доказано в итоге.
Интегральная формула Коши позволяет быстро вычислять интегралы по контуру вокруг точки разрыва, фактически не проводя подробное интегрирование. Достаточно убрать из знаменателя ту скобку 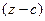 , которая соответствует этой точке разрыва, подставить в остальную функцию
, которая соответствует этой точке разрыва, подставить в остальную функцию 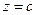 и домножить на
и домножить на 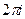 .
.
Обычно она применяется в таком виде:
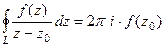
Ведь надо вычислить именно интеграл, который обычно дан без коэффициента, так что коэффициент пишется в другой части равенства.
Пример. Вычислить 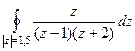 .
.
Решение.Внутри окружности радиуса 1,5 всего одна из двух точек разрыва функции, вторая снаружи. Обозначим в качестве  функцию без
функцию без 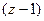 , как будто на
, как будто на 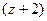 делим чуть раньше, а на
делим чуть раньше, а на 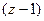 позже.
позже.
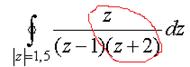
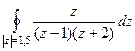 =
= 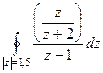 , где
, где 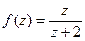 это то, что именно обозначается
это то, что именно обозначается  в интегральной формуле Коши.
в интегральной формуле Коши.
Тогда 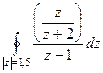 =
= 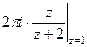 =
= 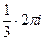 =
= 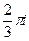 .
.
Ответ. 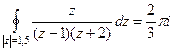 .
.
Теорема 3. (Обобщённая интегральная формула Коши).
Пусть  является аналитической на контуре
является аналитической на контуре 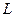 и внутри него, точка
и внутри него, точка 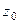 лежит внутри
лежит внутри 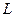 . Тогда
. Тогда 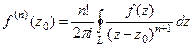 .
.
Доказательство.
Продифференцируем по параметру 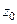 правую и левую часть равенства в исходной интегральной формуле Коши.
правую и левую часть равенства в исходной интегральной формуле Коши.
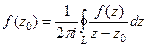 .
.
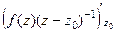 =
= 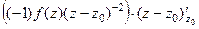 =
= 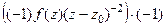 =
= 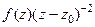 =
= 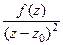 .
.
Таким образом, 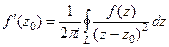 .
.
Следующая производная от 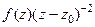 равна
равна
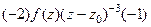 =
= 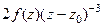 . Аналогично следующая (третья от исходной функции) равна
. Аналогично следующая (третья от исходной функции) равна 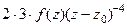 , далее по индукции для n-й производной получим
, далее по индукции для n-й производной получим 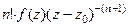 =
= 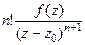 . Тогда
. Тогда 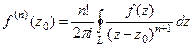 .
.
Рассмотрим примеры, похожие на предыдущий, но в которых будет 2 или 3 степень скобки 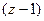 . По обобщённой интегральной формуле Коши, если скобка во 2 степени, надо не просто убрать её из знаменателя, а после этого ещё и один раз продифференцировать оставшуюся функцию, и лишь затем подставлять
. По обобщённой интегральной формуле Коши, если скобка во 2 степени, надо не просто убрать её из знаменателя, а после этого ещё и один раз продифференцировать оставшуюся функцию, и лишь затем подставлять 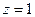 . А если 3 степень, то 2 раза продифференцировать, но с 3-й степени начинает ещё и изменяться коэффициент из-за того, что он уже не равен 1, а будет
. А если 3 степень, то 2 раза продифференцировать, но с 3-й степени начинает ещё и изменяться коэффициент из-за того, что он уже не равен 1, а будет 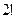 .
.
Пример. Вычислить 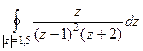 .
.
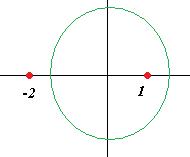
Решение.Окружность радиуса 1,5. Следовательно, точка разрыва 1 внутри, а точка 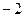 снаружи, поэтому для неё считать не надо.
снаружи, поэтому для неё считать не надо. 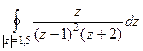 =
= 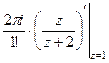 =
= 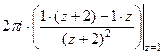 =
= 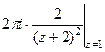 =
= 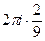 =
= 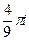 .
.
Ответ. 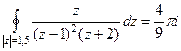 .
.
ЛЕКЦИЯ № 6. 07.10.2020
Дата добавления: 2020-10-14; просмотров: 615;











