Динамика материальной точки. Законы Ньютона.
Первый закон Ньютона
Формулировка: всякое тело находиться в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить состояние.
ИСО – инерциальная система отсчета – система отсчета, в которой выполняется первый закон Ньютона.
При этом, если СО движется равномерно и прямолинейно относительно ИСО, то она также инерциальная СО.
ИСО является гелиоцентрическая СО.
Второй закон Ньютона:
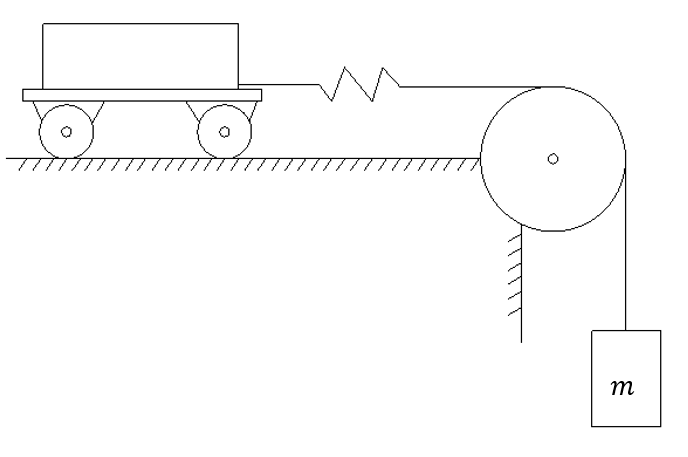
Эксперимент
Результат: при неизменном удлинении пружины тележка будет двигаться равноускорено, при увеличении грузы (приложенной силы) увеличивается ускорение тележки.

|
Если взять другую тележку, то соотношение останется справедливым, но ускорение при аналогичных силах воздействия будут, вообще говоря, другими.
Это объясняется различной «неподатливостью» тележек воздействию силы – инертностью.
Очевидно, что отношение F/a характеризует инертность тела – это масса.
Формулировка: ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально его массе
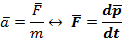
Третий закон Ньютона
Тела 1 и 2 притягиваются друг к другу вследствие того, что, например, несут на себе заряд
Результат: 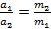
|
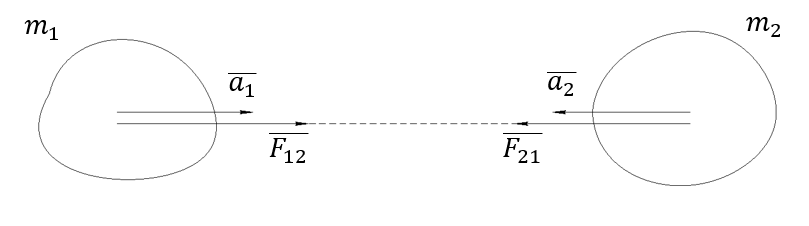
Что в совокупности со вторым законом Ньютона означает равенство сил по модулю и их противоположное направление
Формулировка: всякое действие тел друг на друга носит характер взаимодействия: силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению
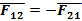
Аксиома(независимости действия сил)
Ускорение, приобретаемое материальной точкой в результате действия на неё системы сил, равно геометрической сумме ускорений, которые бы приобрела данная точка в результате действия на неё сил данной системы в отдельности.
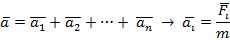
Основное уравнение динамики материальной точки (в векторной форме)
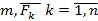
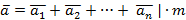
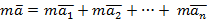
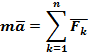
|
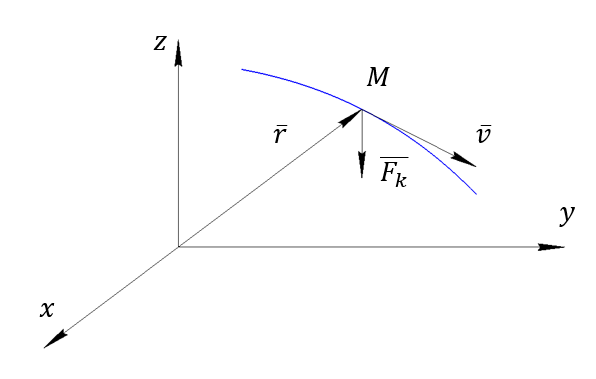
Основное уравнение динамики вращательного движения
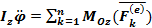 ,
, 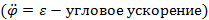
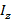 – момент инерции тела относительно оси Oz
– момент инерции тела относительно оси Oz
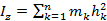 , h - кратчайшее расстояние от k-ой точки до оси Oz
, h - кратчайшее расстояние от k-ой точки до оси Oz
Принцип относительности Галилея
Преобразования Галилея:
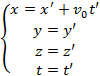
|
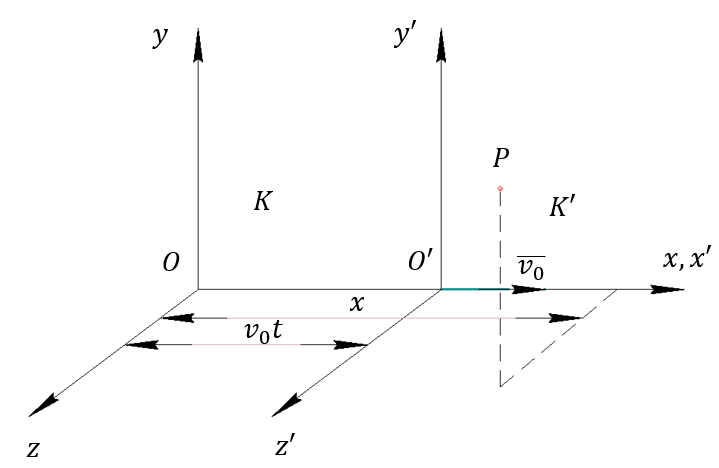
Преобразования Галилея справедливы при 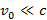
Продифференцировав преобразования Галилея:
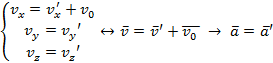
Откуда, согласно второму закону Ньютона, вытекает, что силы, действующие на тело в системах К и К’, одинаковы.
Т.о. уравнения динамики не изменятся при переходе от одной ИСО к другой.
Формулировка: Все механические явления в различных ИСО протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли данная СО или движется равномерно и прямолинейно.
I. Понятие центра масс
Центр масс (ЦМ) – точка в пространстве, положение которой определяется радиус-вектором
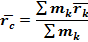
В проекции на оси ДСК: 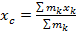 …yc=…zc=…
…yc=…zc=…
Чем хорош ЦМ?
Из () 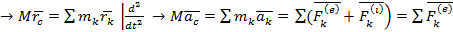
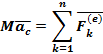
ЦМ механической системы движется как материальная точка, в которой сосредоточена вся масса механической системы, под действием всех внешних сил, приложенных к различным точкам механической системы. (т.н. Теорема о движении ЦМ механической системы)
Методы определения ЦМ:
1) ЦМ находиться в плоскости материальной симметрии системы. Если плоскостей симметрии несколько – на их пересечении.
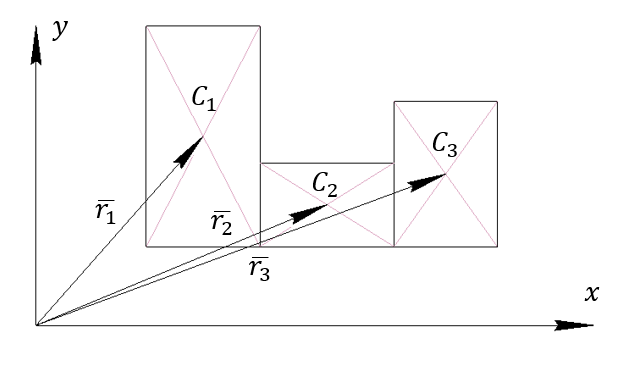
2) Метод разбиения
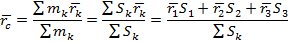
|
3) Метод отрицательных масс
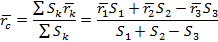
|
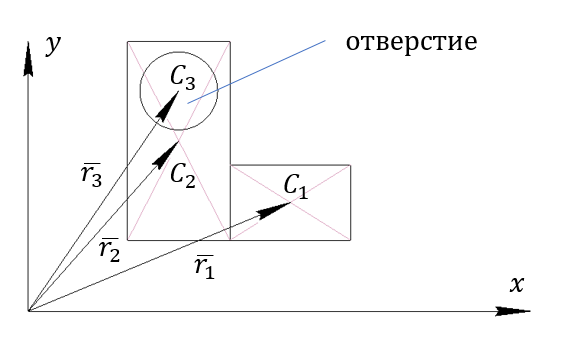
( 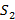 – площадь прямоугольника без отверстия)
– площадь прямоугольника без отверстия)
Замечание: понятие центра тяжести имеет смысл лишь для тех, находящихся в однородном гравитационном поле. В таком случае ЦМ будет являться точкой приложения результирующей силы тяжести.
Теоретический минимум:
1) ИСО. Первый закон Ньютона
2) Инертность и инерция. Второй закон Ньютона
3) Третий закон Ньютона. Принцип суперпозиции сил
4) Принцип относительности Галилея
5) Преобразования Галилея
6) ЦМ. Методы вычисления
| <== предыдущая лекция | | | следующая лекция ==> |
| Принцип работы генератора | | | Правила наложения повязок |
Дата добавления: 2021-10-28; просмотров: 398;











