Формулы вычисления вычетов.
Если  простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета:
простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета: 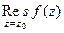 =
= 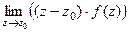 .
.
Если  - полюс порядка m, то верна формула вычисления вычета:
- полюс порядка m, то верна формула вычисления вычета: 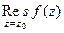 =
= 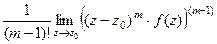 .
.
Они напрямую следуют из обычной и обобщённой интегральных формул Коши. Кстати, первая формула - частный случай второй при 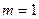 .
.
Пример.Найти вычет 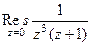 .
.
Решение. Здесь точка 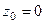 полюс порядка 3, конкретизируем формулу для этого порядка и этой точки:
полюс порядка 3, конкретизируем формулу для этого порядка и этой точки:
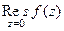 =
= 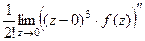 . Итак,
. Итак, 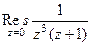 =
= 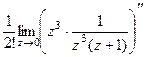 =
= 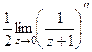 =
= 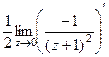 =
= 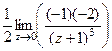 =
= 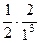 = 1.
= 1.
Пример.Найти вычет 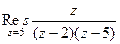 .
.
Решение.Здесь точка 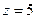 полюс 1 порядка. Поэтому
полюс 1 порядка. Поэтому
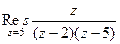 =
= 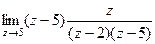 =
= 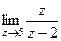 =
=  .
.
Пример *.Найти вычет 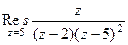 .
.
Решение.Здесь точка 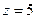 полюс 2 порядка. Поэтому
полюс 2 порядка. Поэтому
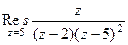 =
= 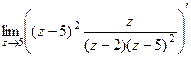 =
= 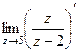 =
=
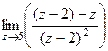 =
= 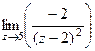 =
= 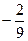 .
.
Основная теорема о вычетах.Если  является аналитической на некотором замкнутом контуре
является аналитической на некотором замкнутом контуре 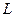 и в области внутри него, за исключением конечного количества изолированных особых точек, то
и в области внутри него, за исключением конечного количества изолированных особых точек, то
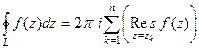 .
.
Доказательство.По интегральной теореме Коши, интеграл по контуру 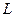 равен сумме интегралов по n контурам внутри него.
равен сумме интегралов по n контурам внутри него.
Тогда 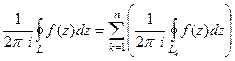 . Но каждое слагаемое в этой сумме - интеграл по контуру вокруг одной особой точки, делённый на
. Но каждое слагаемое в этой сумме - интеграл по контуру вокруг одной особой точки, делённый на
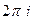 , а по определению это и есть вычет в данной точке
, а по определению это и есть вычет в данной точке 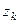 .
.
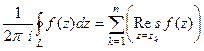
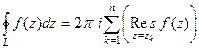 .
.
Вот и получается, что интеграл равен такой величине: 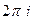 умножить на сумму вычетов.
умножить на сумму вычетов.
Определение вычета в 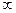 .Пусть
.Пусть 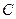 замкнутый контур, на контуре и вне его нет особых точек. Тогда интеграл
замкнутый контур, на контуре и вне его нет особых точек. Тогда интеграл 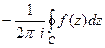 называется вычетом функции
называется вычетом функции 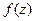 в
в 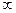 и обозначается
и обозначается 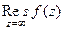 .
.
Когда мы рассматривали конечную точку  , то при вычислении интеграла по контуру обходили его против часовой стрелки, чтобы точка оставалась слева. А чтобы например, линия горизонта (бесконечность) оставалась с левой стороны при движении, нужно круг обходить наоборот, именно по часовой стрелке. Поэтому-то здесь изначально в определении знак минус.
, то при вычислении интеграла по контуру обходили его против часовой стрелки, чтобы точка оставалась слева. А чтобы например, линия горизонта (бесконечность) оставалась с левой стороны при движении, нужно круг обходить наоборот, именно по часовой стрелке. Поэтому-то здесь изначально в определении знак минус.
Теорема (следствие из основной теоремы о вычетах).Если 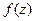 является аналитической во всей комплексной плоскости, за исключением конечного количества изолированных особых точек, то
является аналитической во всей комплексной плоскости, за исключением конечного количества изолированных особых точек, то 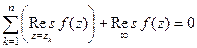 .
.
(Сумма вычетов во всех конечных особых точках + вычет в бесконечности равно 0).
Доказательство.Если в плоскости конечное количество особых точек, то среди них есть самая далёкая от начала координат. Тогда их все можно включить в круг некоторого радиуса. Ограничим все n особых точек замкнутым контуром 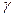 настолько большого радиуса
настолько большого радиуса 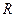 , чтобы все они лежали внутри круга
, чтобы все они лежали внутри круга 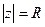 .
.
По определению вычета в 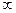 ,
, 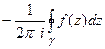 =
= 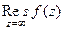 ,
,
а по прошлой теореме, 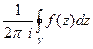 =
= 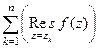 .
.
Получается, что вычет в  противоположен сумме всех вычетов в конечных особых точках. Складывая эти 2 равенства, мы как раз и получим
противоположен сумме всех вычетов в конечных особых точках. Складывая эти 2 равенства, мы как раз и получим 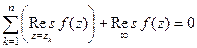 .
.
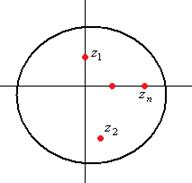
Чертёж. 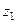 ,
, 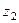 , ...
, ... 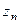 - особые точки.
- особые точки.
Пример. Найти 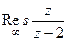 .
.
Решение.Заметим, что в знаменателе только 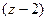 , т.е. эта функция имеет всего лишь одну конечную особую точку. Тогда:
, т.е. эта функция имеет всего лишь одну конечную особую точку. Тогда:
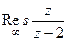 =
= 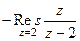 . То есть надо найти вычет в точке 2 и сменить знак.
. То есть надо найти вычет в точке 2 и сменить знак. 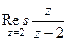 =
= 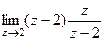 =
= 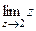 = 2. Поэтому
= 2. Поэтому 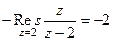 .
.
ЛЕКЦИЯ № 7. 14.10.2020
Приложения вычетов
Дата добавления: 2020-10-14; просмотров: 654;











