Монотонные последовательности

Тема. Функции

Определение (сложная функция):

Пусть задано D,E,G,C,R

На D: y=f(x) с областью значения E

На E: z=g(y) с областью значения G

Тогда на множестве D определена сложная функция z=g(f(x)) с областью значения G. Тогда говорят, что g(f(x)) есть суперпозиция функций g,f.

Пример: Пример

z=sin e^x w=arctgcos e^{xx-ln x}

y=e^x=f(x)

z=sin y=g(y)

D=R

E=R₊

G=[-1;1]

Определение (обратной функции):

Пусть существует D,E,C,R

На D: y=f(x) с областью значений Е. Если для каждого у из y=f(x) найдётся единственный х, то говорят, что на множестве Е задана функция обратная к функции f(x), с областью значений D. Иными словами две функции y=f(x) и x=g(y) являются взаимно обратными если выполняется тождества:

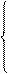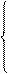y=f(g(y)), " yÎE y=f(g(y)), для любого уÎЕ

Û

x=g(f(x)), " xÎD x=g(f(x)), для любого хÎD

Примеры:

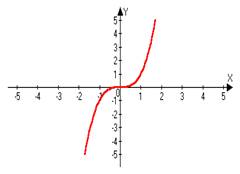
1)y=x³ Û x=³Öy

D=R

E=R

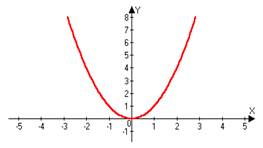2)y=x² Û x=Öy

D=R₊ È{0}=[0;+¥)

E=[0;+¥)

D=R_- È{0}=(-¥;0]

E=[0;¥)Û x=-Öy

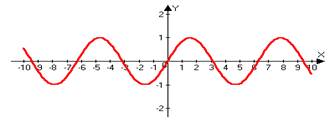3)y=sinx

D=[-p/2;p/2]

E=[-1;1]

x=arcsiny

yÎ[-1;1]; xÎ[-p/2;p/2]

Пусть y=f(x)

D=[a;b]

E=[A;B]

Определение: y=f(x), nÎN

a₁=f(1)

a₂=f(2)

a_n=f(n)

{a_n} – множество значений силовой последовательности nÎN или а_n

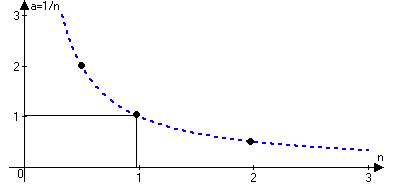{а_n}={1,1/2,1/3,…,1/n,…}

а_n=1/n

{а_n}={sin1;sin2;sinn}

а_n=sinn

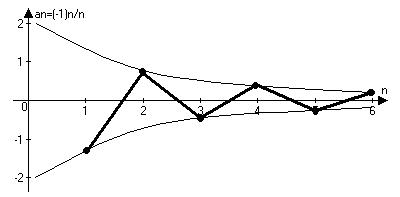
а_n=(-1)ⁿ/n

{(-1)ⁿ}={-1;1;-1;1;-1;1…}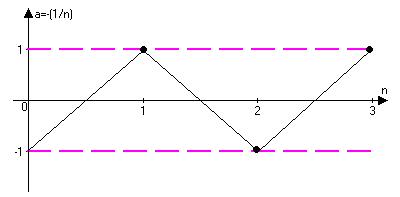

Ограниченные последовательности.

1) Ограниченная сверху, то есть существует В так что а_n£В, для любого nÎN

2) Ограниченная снизу, то есть существует А так что А£b_n, для любого nÎN

3) Ограниченная, то есть существует А,В так что А£а_n£В, для любого nÎN Û существует С>0 так что |а_n|£С, для любого nÎN.

Монотонные последовательности

1) возрастающая a_n<a_n+1, " nÎN

2) убывающая a_n>a_n+1, " nÎN

3) не возрастающая a_n³a_n+1, " nÎN

4) не убывающая a_n£a_n+1, " nÎN

Пределы последовательности.

Определение: числа а , называется пределом числовой последовательности а_n, если для любого сколь угодно малого числа ε>0, найдётся натуральный номер N такой, что для всех чисел n³N выполняется модуль разности |a_n-a|<ε Û " ε>0 $ N : " n³N Þ|a_n-a|<ε.

Начиная с этого номера N все числа этой последовательности попадают в ε окрестность числа а. Другими словами начиная с номера N вне интервала а-ε;а+ε может находиться не более конечного числа членов последовательности.

Lim a_n=0

^n®¥

Примеры: Доказать, что ln(-1)²/n=0

Зададим любое ε>0, хотим чтобы |(-1)ⁿ-0|<ε, начиная с некоторого номера N, 1/n<ε Þ n>1/ε

N=[1/ε]+1

ε=0.01

N=[1/0.01]+1=101

|a_n|<0.01, если n³101

* * *

a_n=1-1/n²

lim(1-1/n²)=1

^n®+¥

Для любого ε>0 |(1-1/n²)-1|<ε

|-1/n²|<ε Þ 1/n²<ε Þ n²>1/ε Þ n>1/Öε

N=[1/Öε]+1

Лекция №3