Первый замечательные пределы.

Терема lim (sin(x)/x)=1

^x®0

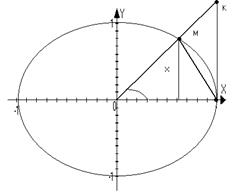Доказательство:

S_∆OMN=1/2 sin(x)

S_секOMN=1/2(x)

S_∆OKN=1/2 tg(x)

S_∆OMN<S_секOMN< S_∆OKN

1/2sin(x)<1/2(x)<tg(x)

sin(x)<x<tg(x)

1<x/sin(x)<1/cos(x)

lim (1-cos(1/n))=0

^n®+¥

lim (1-cos(x))=0 Þ lim (cos(x))=1

^{x®0 x®0}

lim (x/sin(x))=0

^x®0

x>0

lim (x/sin(x))=1

^x®0

lim(1/(x/sin(x)))= lim(sin(x)/x)=1 что и требовалось доказать

^{x®0 x®0}

Определение бесконечного предела и пределов при х®+¥.

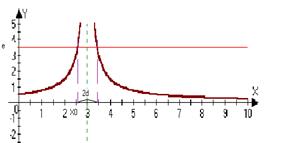lim (f (x))=+¥ Û "ε>0 $d>0: " xÎO°_d(x₀)Þf(x)ÎO_ε(+¥)

^x®x_°

"(x): 0<|x-x₀|<d

(////////// x

ε

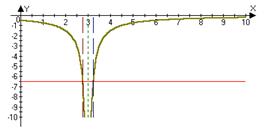lim (f (x))=-¥ Û "ε>0 $d>0: " xÎO°_d(x₀)Þf(x)ÎO_ε(-¥)

^x®x_°

"(x): 0<|x-x₀|<d

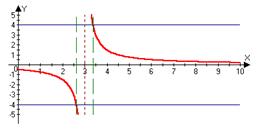lim (f (x))=¥ Û "ε>0 $d>0: " xÎO°_d(x₀)Þf(x)ÎO_ε(¥)

^x®x_°

|f(x)|>ε

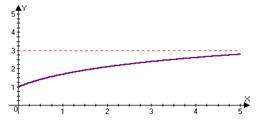lim (f (x))=b Û "ε>0 $∆>0: " xÎO_∆(+¥)Þf(x)ÎO_ε(b)

^x®+¥

" x: x>∆ |f(x)-b |<ε

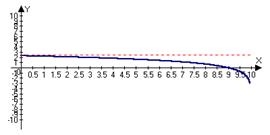lim (f (x))=b Û "ε>0 $∆>0: " xÎO_∆(-¥)Þf(x)ÎO_ε(b)

^x®-¥

" x: x<-∆ |f(x)-b |<ε

Односторонние пределы.

Определение

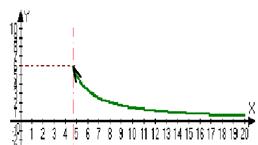
f(x) определена в O°⁺(x₀)

lim (f (x))=b Û "ε>0 $d>0: " xÎO°⁺_d(x₀)Þf(x)ÎO_ε(b) x₀<x<x₀+d

^x®x_°⁺⁰

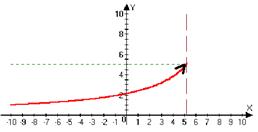Определение

f(x) определена в O°^-(x₀)

lim (f (x))=b Û "ε>0 $d>0: " xÎO°^-_d(x₀)Þf(x)ÎO_ε(b) x₀-d<x<x₀d

^x®x_°^-0

Теорема Пусть f(x) определена в O°(x₀) Для того чтобы существо-

вал предел $ lim(f(x))=b Û $ lim(f(x))=lim(f(x))=b

^x®x_° ^x®x_°^{+0 x®x}_°^-0

Пусть $ lim(f(x))=b, то есть "ε>0 $d>0: " xÎO°_d(x₀)Þf(x)ÎO_ε(b) f(x)ÎO_d(b) для " xÎO°⁺_d(x₀) и для " xÎO°^-_d

^x®x_°

" xÎO°^-_d(x₀)Þ$ lim(f(x));lim(f(x))=b что и требовалось доказать.

^x®x_°^{+0 x®x}_°^-0