Влияние сечения нулевого провода на потери активной мощности и уравновешивание токов нулевой последовательности

Чтобы понять, как влияет сечение нулевого провода на величину потерь активной мощности, соотношение активных сопротивлений нулевого и линейного проводов будем считать переменными величинами, а значения модулей линейных токов и тока в нулевом проводе – фиксированными.

Отношение модуля тока обратной последовательности к модулю тока нулевой последовательности обозначим a, а нагрузки фаз принимаем однородными. В этом случае потери активной мощности участка четырехпроводной сети, отнесенные к потерям только от ТНП, численно равны коэффициенту неравномерности загрузки фаз (КНЗ):

.

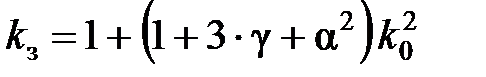Наиболее широко используются в инженерной практике сети, у которых значение γ = 2, прежде всего, в промышленных распределительных сетях 0,4 кВ. Сечение нулевого провода в 2 раза меньше сечения фазного провода. В коммунальных распределительных сетях стали использовать сети, у которых нулевой и фазный провод имеют одинаковое сечение, т.е. γ = 1, а в зарубежной практике при использовании сетей с несущими нулевыми проводами сечение нулевого провода принимают даже в 2 раза больше сечения фазного провода (γ = 0,5).

Если КНУ равен нулю, то k_з = 1. В этом случае КНЗ не зависит от соотношений сечений нулевого и фазного проводов, а также от отношения КНТ к КНУ. Когда линейные токи симметричны, эти факторы не имеют никакого значения.

Для самого тяжелого случая несимметричного режима, когда вся нагрузка однофазная и включена в одну из фаз трёхфазной сети (k₀ = 1) зависимость КНЗ от a и g представляет собой уравнения поверхностей второго порядка: k_з = 2 + 3 · γ + α² (рис. 13.1). Если k₀ = 0,5, то k_з = 1,5 + 1,5 · γ + 0,5 · α².

Как следует из последнего уравнения параболического цилиндра, тангенс его угла j наклона к оси 0g уменьшился и стал равен 1,5.

Для симметричного режима условию k₀ = 0 на (рис. 13.1) соответствует часть плоскости 1, d, h, e, параллельной координатной плоскости g, 0, a и расположенной в первом октанте.

На (рис. 13.1) в пространстве между полостью a, b, c, 2 и частью плоскости d, e, 1 в первом октанте для фиксированных значений k₀, в интервале от 0 до 1, располагается множество поверхностей второго порядка (наклонённых к оси 0g параболических цилиндров). Полость a, b, c, 2 при условии перехода от крайнего случая несимметричного режима (вся нагрузка трехфазной сети включена на одну фазу) к симметричному режиму (нагрузка равномерно распределена между фазами или парами фаз сети) как бы скользит по оси 0k_з вниз от k₃ = 2 до k_з = 1. При этом полости параболических цилиндров становятся всё более пологими по мере приближения их к плоскости d, e, 1, а тангенс угла j наклона направляющих параболических цилиндров уменьшается. При k₀ = 0 параболический цилиндр вырождается в плоскость.

Рис. 13.1. График зависимости КНЗ от a и g для случая несимметричного режима, когда вся нагрузка однофазная и включена в одну из фаз трёхфазной сети

На (рис. 13.2) показана зависимость КНЗ от a при фиксированных значениях g, когда k₀ = 1. Представлены следы на плоскостях, параллельных плоскости k_з, 0, a, спроецированные на неё.

При g = 0,5; g = 1,0; g = 2 получим соответственно семейство парабол (см. рис. 13.2):

k_з = 8 + α²; k_з = 5 + α²; k_з = 3,5 + α².

Область между отрезками прямой k₃ = 1, параллельной оси абсцисс, и верхней параболы является областью изменения всех возможных значений КНЗ в зависимости от a. Она охватывает всё бесконечное множество режимов линейных токов, от симметричного режима до режима, когда вся нагрузка включена в одну из фаз трёхфазной сети. С увеличением сечения нулевого провода она сужается. При этом значения g уменьшаются.

Рис. 13.2. График зависимости КНЗ от a при фиксированных значениях g, когда k₀ = 1

Относительные потери активной мощности на участке четырехпроводной сети существенно зависят от соотношения ТОП и ТНП. Причём, главенствующая роль в этом соотношении принадлежит ТНП.

При амплитудной несимметрии k₂ = k₀, поэтому

k_з = 1 + (2 + 3 · γ) · k₀².

Если система линейных токов уравновешена, то k₀ = 0, а k_з = 1.

Когда же k₀ = 1 (нагрузка включена на одну фазу), то k_з = 3 · (1 + γ).

Последнее равенство представляет собой уравнение прямой. Если γ изменяется в интервале 0 … 2, то k_з - в интервале 3 … 9. Заштрихованная область между отрезками прямых на (рис. 13.3) в интервале изменений γ от 0 до 2 представляет собой область всех возможных значений k_з для соответствующих им значений γ и k₀. Причем значения γ > 2 нет смысла брать для рассмотрения в силу требований ПУЭ к нулевым проводам ВЛ 0,4 кВ. Реально сопротивление нулевого провода ВЛ 0,4 кВ не может иметь значение, равное нулю, поэтому у графиков семейства характеристик k_з(γ) не показано их пересечение с осью ординат. Тем не менее, можно отметить, что ордината точки пересечения верхней прямой с осью 0γ равна трем, а ордината точки пересечения нижней прямой с осью ординат равна единице. С уменьшением несимметрии нагрузок наклон отрезков прямых k_з(γ) уменьшается пропорционально отношению утроенного значения квадрата модуля тока в нулевом проводе к квадрату суммы линейных токов фаз на головном участке ВЛ 0,4 кВ. Место нахождения отрезков прямых k_з(γ) внутри заштрихованной области определяется также величиной квадрата отклонения среднеквадратичного тока фаз на головном участке ВЛ 0,4 кВ к их среднему значению. Чем круче наклон отрезков прямых k_з(γ), тем больше абсолютное значение k_з для одного и того же γ. Поскольку k_з ≡ γ, то одним из целесообразных мероприятий по экономии электроэнергии в сетях 0,4 кВ с несимметричными нагрузками следует признать увеличение проводимости нулевых проводов до величины, равной или даже больше, чем у фазных проводов. Например, для предельного случая включения всей нагрузки на одну фазу k_з = 6 при γ = 1, k_з = 9 при γ = 2. В этом случае потери от несимметрии нагрузок (без перераспределения их между фазами) для γ = 1 (R_F = R_N) на одну треть меньше, чем для γ = 2 (R_F = R_N / 2). Естественно, что вывод, сделанный здесь для максимального значения k₀, возможно распространить на всю заштрихованную область в интервале изменения γ от 1 до 2.

Рис. 13.3. Область всех возможных значений k_з для соответствующих им значений γ и k₀

Разница в стоимости проводов при переходе от одного сечения к следующему большему и стоимость монтажных работ по подвеске 1 км провода примерно одинаковы. Стоимость потерь электроэнергии до замены нулевого провода в полтора раза больше годовых затрат на мероприятия по замене провода на ближайшее большее сечение. Поэтому уже на стадии проектирования следует предусматривать установку нулевого провода такого же сечения, как у фазного. Благодаря незначительной разнице в стоимости проводов, отпадает необходимость иметь два сечения проводов, что является одним из неоспоримых преимуществ при производстве электромонтажных работ.

Увеличение сечения нулевого провода является гарантированным мероприятием по снижению потерь электроэнергии, вызванных несимметричными однофазными нагрузками.