Тема: Сравнение бесконечно больших и бесконечно малых.

Определение.

Пусть a(x) и b(x) – бесконечно малые при х®х₀ (±¥)

1) a(x) ~ b(x) при х®х₀ (±¥) если lim a(x)/b(x)=1 ^{x®x0 (±¥)}

2) a(x) и b(x) одинакового порядка при х®х₀ (±¥) если lim a(x)/b(x)=с¹0 ^{x®x0 (±¥)}

3) a(x) бесконечно малое более высокого порядка малости чем b(x) при х®х₀ (±¥) если lim a(x)/b(x)=0 ^{x®x0 (±¥)}

Определение.

Пусть f(x) и g(x) – бесконечно большое при х®х₀ (±¥)

1) f(x) ~ g(x) при х®х₀ (±¥) если lim f(x)/g(x)=1 ^{x®x0 (±¥)}

2)f (x) и g (x) бесконечно большие одинакового порядка роста, если при х®х₀ (±¥) если limf(x)/g(x)=с¹¥ ^{x®x0 (±¥)} <¥

В частности, если с=1, то они эквивалентны

1) f (x) бесконечно большое более низкого порядка роста чем g (x) или иначе g(x) бесконечно большое более высокого порядка роста чем g(x) при х®х₀ (±¥) если lim f (x)/g (x)=0 ^{x®x0 (±¥)}

Примеры:

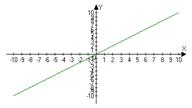
1) 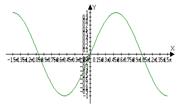sin(x) – бесконечно малое

x при х®х₀ – бесконечно малое

Сравним их lim sin(x)/x=1 Û sin(x)~x

^x®0

при х®0

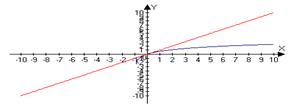2) 1n(1+x) – бесконечно малое

х при х®0 – бесконечно малое

Сравним их lim ln(1+x)/x= lim ln(1+x)^1/x =1 Û

^{x®0 x®0}

ln(1+x) ~ x, при х®0

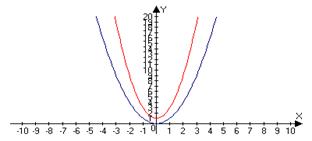3) x² – бесконечно большие

2х²+1, при х®+¥ – бесконечно большие

Сравним lim x²/(2x²+1) = lim x²/x²(2+1/x²)=1/2

^{x®+¥ x®+¥}

то есть функция является бесконечно большой и

одинакового порядка. Замечание: если одну из

функций одинакового порядка роста домножить на

одинаковую const, то они станут эквивалентны.

Определение:

1) пусть a(х)=оb(х) – бесконечно малое при х®х₀(±¥). То мы говорим, что a(х) и b(х) при х®х₀ (±¥), если a(х)=g(х)b(х), бесконечно малое при х®х₀ (±¥). Другими словами - a(х) – бесконечно малое более высокого порядка, чем b(х) така как a(х)/b(х)=g(х) – бесконечно малое, то есть lim a(x)/b(x)=0 ^{x®0 (±¥)}

2) пусть fa(х)=оgb(х) – бесконечно большое при х®х₀(±¥). То мы говорим, что fa(х) и g (х) при х®х₀ (±¥), если f (х)=g(х)g (х). Другими словами - f (х) – бесконечно большое более низкого порядка, чем g(х) так как f(х)/g (х)=g(х) – бесконечно малое, то есть lim f (x)/g (x)=0 ^{x®0 (±¥)}