Связь между бесконечно большими и бесконечно малыми величинами.

Теорема:

1)a_n- бесконечно большая Þ 1/a_n – бесконечно малая

2)a_т – бесконечно малая, a_n¹0 ("n>N₀) Þ1/a_n – бесконечно большая

Доказательство:

1)a_n- бесконечно большая Þ lim a_n=¥ Þ для достаточно больших номеров n a_n¹0. Зададим любое сколько

^n®+¥

угодно малое ε>0, положим ε=1/ε>0

Для ε $N₁:"n>N₁Þ |a_n|>ε, то есть |a_n|>1/ε N=max{N₁;N₀}

Тогда "n>N Þ 1/|a_n|<ε, то есть lim 1/a_n=0, то есть 1/a_n – бесконечно малое

^n®+¥

2)a_n – бесконечно малоеÞ lim a_n=0

^n®+¥

Дано: a_n¹0, n>N₀ зададим "ε>0 положим ε=1/ε>0

$N₁:"n>N₁Þ |a_n|<ε=1/ε

N=max{N₀;N₁}: "n>N Þ 1/|a_n|=¥, то есть 1/a_n – бесконечно большая.

Основные теоремы о существование предела последовательности.

Теорема Вейрштрасса:

Пусть a_n- ограниченная и моннатонна. Тогда $ lim a_n=а<¥

^n®+¥

Лемма. Среднее арифметическое чисел больше среднего геометрического. Равенство достигается только если все числа равны.

Лекция №5

Тема: Бесконечно большие последовательности

Теорема:

lim(1-1/n)ⁿ=1/e e=2,7183

^n®+¥

0£a_n=1-1/n£1 "nÎN, то есть a_n=(1-1/n)ⁿ- ограниченна.

ⁿ⁺¹Öa_n=ⁿ⁺¹Ö(1-1/n)ⁿ·1=ⁿ⁺¹Ö(1-1/n)(1-1/n)…(1-1/n)·1<[1+(1-1/n)+…+(1-1/n)]/n+1=(n+1-n·1/n)/n+1=n/n+1=1-1/n+1

ⁿ⁺¹Ö(1-1/n)ⁿ<1-1/n+1

(1-1/n)ⁿ<(1-1/n+1)ⁿ⁺¹

a_n<a_n+1 "nÎN Þ последовательность возрастает и ограниченная.

(1-1/n)ⁿ – имеет конечный предел

lim(1-1/n)ⁿ=1/e

^n®+¥

Следствие

lim(1+1/n)ⁿ=e

^n®+¥

lim1/(1+1/n)ⁿ=(n/n+1)ⁿ=[1-1/(n+1)]ⁿ⁺¹/ [1-1/(n+1)]=(1/e)/1=1/e

^n®+¥

lim[1/(1+1/n)ⁿ]=1/e

^n®+¥

lim(1+1/n)ⁿ=e

^n®+¥

Определение под последовательности

Пусть дана a_n зададим произвольный набор натуральных чисел таких, что

n₁<n₂<n₃<…<n_k<….

a_n1,a_n2,…,a_nk,…

Полученная последовательность называется под последовательностью и сходной последовательности.

a_n=(-1)ⁿ

{a_n}={-1;1;-1;1….}

n₁=2;n₂=4,….,n_k=2k

{a_nk}={1,1,1,1…}

Теорема

Пусть последовательность a_n сходится, тогда "последовательности

$ lim a_n=a "{a_nk} – гас и lim

^n®+¥

lim a_nk=0

^n®+¥

Доказательство так как a_n – сходиться, то "ε>0 $N: "n>N Þ |a_n-a|<ε

a_nk; n_k>N то есть |a_nk-a|<ε

Пример

a_n=(-1)ⁿ – не имеет предела

{a_2n}={1,…,1,…,}

{a_2n-1}={-1,….,-1,…}

имели бы тот же самый предел.

Предел функции.

Определение

Пусть y=f(x) определена в O°(x₀). Мы говорим, что функция f(x) имеет предел в при х®х₀ если "ε>0 $ d>0

"x:0<|x-x₀|<dÞ |f(x)-b|<ε

lim f(x)=b

^x®x_°

Через окрестности это определение записывается следующим образом

"ε>0 $d>0 "xÎ0°_d(x₀)Þf(x)Î0_ε(b)

Если lim f(x)=0, то f(x) наз бесконечно малой при x®x₀.

^x®x_°

Замечание. Необходимо указать в каком именно процессе f(x) бесконечно малое. Надо указать к какому числу ® а.

f(x)=x-1

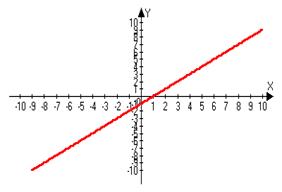
1.x®1 lim(x-1)=0, то есть y=x-1 бесконечно малое при x®1

^x®1

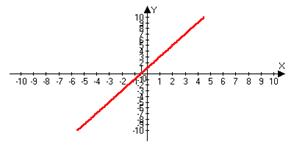2.x®2 lim(x-1)=1, то есть y=x-1 не является бесконечно малой при x®2

^x®1

Пример

f(x)=2x+1 x®1

Докажем lim(2x+1)=3

^x®1

"ε>0 $d>0 "x:0<|x-1|<dÞ |(2x+1)-3|<ε

|(2x+1)-3|<ε

|x-1|<ε/2

x¹1

Положим d=ε/2

Теорема о бесконечно малом

1)a(x);b(x) – бесконечно малое x®x₀ Þ a(x)+b(x) – бесконечно малое при x®x₀

2)a(x);b(x) – бесконечно малое при x®x₀

3)Если f(x) – ограниченна в O°(x₀) и a(x) – бесконечно малое при x®x₀, то f(x);a(x) – бесконечно малое при x®x₀

Доказательство (3)

Так как f(x) – ограниченна в O°(x₀), то $ С>0: "xÎO°(x₀)Þ|f(x)|£C;

Так как a(x) – бесконечно малое при х®х₀, то "ε>0 $d>0 "x: 0<|x-x₀|<d Þ |a(x)|<ε "ε₁>0

Положим ε=ε₁/c

$d>0 "x: 0<|x-x₀|<dÞ |f(x)a(x)|=|f(x)||a(x)|<Cε=ε₁Þ lim f(x)a(x)=0, то есть f(x)a(x) – бесконечно малое при x®x₀

^x®x_°

Лекция №6