Свойства бесконечно малой последовательности.

Теорема. Сумма бесконечно малой есть бесконечно малое.

a_nb_n®бесконечно малое Þ a_n+b_n – бесконечно малое.

Доказательство.

Дано:

a_n- бесконечно малое Û "ε>0 $ N₁:"_n>N₁ Þ |a_n|<ε

b_n- бесконечно малое Û "ε>0 $ N₂:"_n>N₂ Þ |b_n|<ε

Положим N=max{N₁,N₂}, тогда для любого n>N Þ одновременно выполняется оба неравенства:

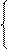
|a_n|<ε |a_n+b_n|£|a_n|+|b_n|<ε+ε=2ε=ε₁"n>N

|b_n|<ε

Зададим "ε₁>0, положим ε=ε₁/2. Тогда для любого ε₁>0 $N=maxN₁N₂ : " n>N Þ |a_n+b_n|<ε₁ Û lim(a_n+b_n)=0, то

^n®¥

есть a_n+b_n – бесконечно малое.

Теорема Произведение бесконечно малого есть бесконечно малое.

a_n,b_n – бесконечно малое Þ a_nb_n – бесконечно малое.

Докозательство:

Зададим "ε₁>0, положим ε=Öε₁, так как a_n и b_n – бесконечно малое для этого ε>0, то найдётся N₁: " n>N Þ |a_n|<ε

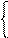$N₂: " n>N₂ Þ |b_n|<ε

Возьмем N=max {N₁;N₂}, тогда "n>N = |a_n|<ε

|b_n|<ε

|a_nb_n|=|a_n||b_n|<ε²=ε₁

" ε₁>0 $N:"n>N |a_nb_n|<ε²=ε₁

lim a_nb_n=0 Û a_nb_n – бесконечно малое, что и требовалось доказать.

^n®¥

Теорема Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность

а_n – ограниченная последовательность

a_n –бесконечно малая последовательность Þ a_na_n – бесконечно малая последовательность.

Доказательство: Так как а_n – ограниченная Û $С>0: "nÎN Þ |a_n|£C

Зададим "ε₁>0; положим ε=ε₁/C; так как a_n – бесконечно малая, то ε>0 $N:"n>NÞ |a_n|<εÞ |a_na_n|=|a_n||a_n|<Cε=C·ε₁/C=ε₁

"ε₁>0 $N: "n>N Þ |a_na_n|=Cε=ε₁ Þ lim a_na_n=0Û a_na_n – бесконечно малое

^n®¥

Замечание: в качестве ограниченной последовательности можно рассматривать const Þ произведение постоянно.

Теорема о представление последовательности имеющий конечный предел.

lim a_n=a Û a_n=a+a_n

^n®+¥

Последовательность a_n имеет конечный предел а тогда и только тогда, когда она представлена в виде a_n=a+a_n

где a_n – бесконечно малая.

Доказательство:

lim a_n Û " ε>0 $N:"n>N Þ |a_n-a|<ε. Положим a_n-a=a_n Þ |a_n|<ε, "n>N, то есть a_n - бесконечно малая

^n®+¥

a_n=a+a_n что и требовалось доказать

Доказательство (обратное): пусть a_n=a+a_n, a_n – бесконечно малая, то есть a_n=a_n-a Û "ε>0 $N: "n>N Þ

Þ|a_n|=|a_n-a|<ε, то есть lim a_n-а

^n®+¥