Рівняння Лагранжа першого роду

Розглянемо невільну матеріальну систему, що складається з n матеріальних точок. На систему накладено h голономних в’язей. Число ступенів вільності цієї системи визначається формулою

s=2n - h.

Якщо в’язі задані рівняннями

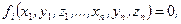(18.11)

де і=1,2,3,...,h, то рівняння Лагранжа першого роду мають, вигляд

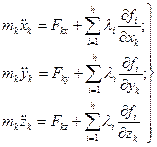(18.12)

(k=1, 2,...,n; і =1, 2,...,h),

де F_kx, F_ky, F_kz - проекції на осі х, у, z рівнодійної активних сил, прикладених до k-тої матеріальної точки, λ_і - невизначені множники. Рівняння Лагранжа першого роду інколи називають рівняннями Лагранжа з множниками. Ці 3n рівнянь (18.12) спільно з h рівняннями в’язей утворюють систему 3n+h рівнянь з 3n+h невизначеними невідомими (3n координат, n матеріальних точок і h невизначених множників).

В рівняннях (18.12) виразимо:

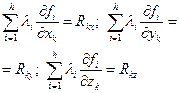(18.13)

( k=1, 2,...,n; і=1, 2,...,h),

де R_kx, R_ky, R_kz - проекції на вісі x, у, z рівнодійної реакцій в’язей, які діють на k-ту матеріальну точку.

Задачу на визначення законів руху точок системи і реакцій в’язей за допомогою рівнянь Лагранжа першого роду рекомендується розв’язувати в такій послідовності:

1) показати на рисунку активні сили;

2) вибрати систему декартових осей координат;

3) визначити проекції F_kx, F_ky, F_kz активних сил, прикладених до матеріальних точок, на декартові осі координат ;

4) скласти рівняння в’язей, накладених на матеріальні точки системи f_і=0 (і=1, 2,...,h);

5) обчислити частинні похідні від рівняннь в’язей за декартовими координатами матеріальної точки:

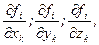де і=1, 2,...,h; k=1, 2,...,n;

6) скласти систему 3n рівнянь Лагранжа першого роду, в які ввійдуть h невизначених множників λ₁, λ₂,..., λ_h;

7) вибрати рівняння кількістю, рівною h, розв’язати ці рівняння відносно λ₁, λ₂,..., λ_h;

8) підставити одержані в пункті 7) значення h множників λ_і в останні 3n-h рівнянь Лагранжа першого роду;

9) приєднати до цих 3n-h рівнянь Лагранжа h рівнянь в’язей та інтегруванням визначити закон руху матеріальної точки (або точок матеріальної системи);

10) визначити проекції реакцій в’язей 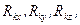де k=1, 2,...,n.

Зауваження. Для закріплення матеріалу §18 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 47.1 - 47.7, 48.1, 48.3 - 48.7;

2) № 47.9 - 47.13, 47.15, 48.8, 48.9, 48.12, 48.16, 48.17, 48.21, 48.26 - 48.31, 48.41, 48.43;

3) № 47.16 - 47.19, 48.20, 48.24, 48.33, 48.34, 48.44, 48.46, 48.47 – 48.50, 48.52.

Рекомендується розв’язати також задачі № 12.2 - 12.4, 12.6, 12.10, 12.11, 12.18, 12.19, 12.21 - 12.24, 12.26, 12.29, 12.30 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Запишіть загальне рівняння динаміки механічної системи.

2. Як обчислюють роботу сил інерції на можливих переміщеннях точок тіла при його поступальному, обертальному і плоскому рухах?

3. Які задачі можна розв’язати за допомогою загального рівняння динаміки?

4. Запишіть загальне рівняння динаміки механічної системи в узагальнених координатах.

5. Яка послідовність розв’язання задач за допомогою загального рівняння динаміки?

6. Які додаткові правила дозволяють полегшити розв’язання задач за допомогою загального рівняння динаміки?

7. Запишіть загальний вигляд рівнянь Лагранжа другого роду.

8. Який вигляд мають рівняння Лагранжа другого роду, якщо всі активні сили є потенціальними?

9. Що називають функцією Лагранжа?

10. Як записати рівняння Лагранжа другого роду, враховуючи функцію Лагранжа?

11. Сформулюйте план розв’язування задач за допомогою рівнянь Лагранжа другого роду.

12. Запишіть рівняння Лагранжа першого роду для невільної матеріальної системи, на яку накладені голономні в’язі.

13. Покажіть порядок розв’язання задач на визначення законів руху точок системи за допомогою рівнянь Лагранжа першого роду.