Рiвняння Мещерського

Розглянемо матерiальну систему, обмежену поверхнею S. Маса в поверхнi S змiнюється за заданим законом m = m(t), тобто задана функцiєю часу (рис. 13.1).

Рис. 13. 1.

Запишемо теорему про змiну кiлькостi руху системи:

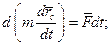
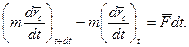(13.15)

Позначимо абсолютну швидкість центра мас всередині поверхні S в момент 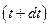через 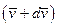. Нехай 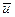– абсолютна швидкість викинутих частинок з масою 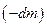. В цих позначеннях рівняння (13.12) перепишемо так:

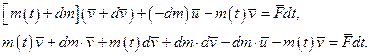
Нехтуючи величиною dm×d 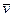, одержимо:

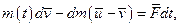
звiдси

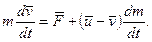(13.16)

Величина 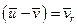є по вiдношенню до рухомої точки вiдносною швидкiстю викинутих частинок. Тодi

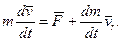(13.17)

Величина

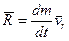
називається реактивною силою.

Рiвняння (13.17) називають рiвнянням Мещерського.

Якщо вiдносна швидкiсть 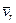= 0 , то 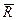= 0 i рiвняння (13.17) приймає вигляд:

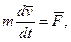
це другий закон Ньютона.

Якщо абсолютна швидкiсть викинутих частинок 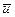= 0, то з (13.16) одержимо:

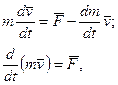
що по формi також спiвпадає з другим законом Ньютона.

13. 5. Задачi Цiолковського.

Перша задача. Визначити швидкiсть v руху ракети, якщо вiдносна швидкiсть v_r витiкання газiв постiйна за модулем i направлена в бік, протилежний руховi ракети. Ракета з безперервним витiканням газiв летить вертикально вгору. Опором повiтря i силою ваги нехтуємо.

Розглядаємо ракету як точку змiнної маси i запишемо рiвняння Мещерського для випадку :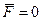

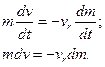
Роздiлимо змiннi

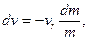
проiнтегруємо

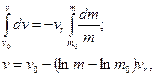
де v₀- початкова швидкiсть ракети; m₀- початкова маса ракети.

Значить

v = v₀ + v_rln(m₀/m). (13.18)

Ця формула називається формулою Цiолковського. Нею можна користуватися для наближеного обчислення швидкостi ракети в тих випадках, коли сила опору i сила ваги не є великими порiвняно з реактивною силою.

Розв’яжемо таку задачу. Яким повинно бути вiдношення початкової маси ракети до маси в кiнцi горіння пального для досягнення ракетою першої космiчної швидкостi, якщо вiдносна швидкiсть викидання частинок постiйна i дорiвнює 3000 м/с?

Дано: v = 7910 м/с; v₀ = 0; v_r = 3000 м/с.

Знайти: m₀/m.

Розв’язання. По формулi Цiолковського маємо:

7910 = 3000ln(m₀/m); ln(m₀/m) = (7910/3000) = 2,64;

(m₀/m) = e^2,64; (m₀/m) = 14,0.

Значить, m₀ = 14,0 m: стартова вага ракети повинна бути в 14 разiв бiльша за вагу останнього ступеня ракети.

Друга задача. Ракета рухається в однорiдному полi сил ваги вертикально вгору з постiйним прискоренням а. Ефективна швидкiсть витiкання газiв v_r постiйна. Визначити: 1) закон змiни маси ракети; 2) час Т, за який маса ракети зменшиться в 2 рази.

Розглянемо рух ракети, запущеної з поверхнi Землi в системi координат з початком в точцi запуску (рис. 13.2).

Рiвняння Мещерського запишемо так:

Рис. 13. 2.

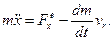
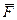Сила представляє собою результуючу складання сили притягання i сили аеродинамiчного опору

атмосфери. Реактивна сила

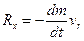
направлена в бiк додатного напряму осi х, бо (dm/dt)<0. Введемо позначення: S - площа вихiдного перерiзу сопла; Р - тиск в газовому потоцi на зрiзi сопла; р(х) - статичний атмосферний тиск.

Сила, обумовлена тиском газового потоку i статичним тиском атмосфери, дорiвнює (Р- р(х)).

Тоді сила тяги двигуна ракети

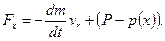
При русi в пустотi р(х) = 0 i

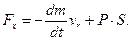
Це спiввiдношення запишемо так:

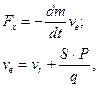
де

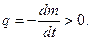
Величина v_e>v_r називається ефективною швидкiстю витiкання.

Таким чином, рух ракети описується рiвнянням:

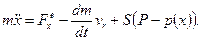(13.19)

Розв’язок цього рiвняння є складним. При вiдсутностi атмосфери з (13.19) одержимо:

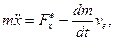(13.20)

де 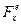- сила тяжiння.

Якщо знехтувати силою тяжiння i силою опору атмосфери, то з (13.20) маємо:

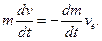
Звідси

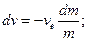
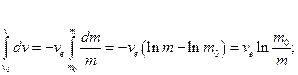
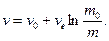(13.21)

Позначимо z = (m₀/m) - це число Цiолковського.

У випадку нашої задачi рiвняння (13.20) записуємо так:

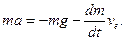
Роздiлимо змiннi

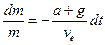
та проінтегруємо

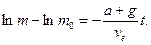
Звiдси

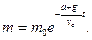
При m = m₀/2, t = T:

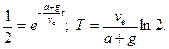
Якщо ракета рухається при g = 0 (полe тяжiння вiдсутнє), то

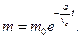
Зауваження. Для закріплення матеріалу §13 (пункти 13.2 – 13.5) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 36.1 - 36.6, 45.2, 45.4;

2) № 36.7 - 36.9, 36.11 - 36.13, 45.8 - 45.12, 45.16, 45.18 – 45.20, 45.27;

3) № 36.10, 36.14, 45.22 – 45.24, 45.26, 45.28, 45.29, 45.34.

Рекомендується розв’язати також задачі № 9.4, 9.5, 17.2 - 17.8 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Як формулюється теорема про зміну кількості руху матеріальної системи?

2. Що називають кількістю руху матеріальної системи?

3. Як кількість руху матеріальної системи виражається через швидкість центра мас?

4. Як записується теорема про зміну кількості руху матеріальної системи в проекціях на декартові вісі координат?

5. Сформулюйте наслідки теореми про зміну кількості руху матеріальної системи.

6. Запишіть теорему про зміну кількості руху матеріальної системи в інтегральній формі.

7. Як теорема про зміну кількості руху системи в інтегральній формі записується в проекціях на декартові осі координат?

8. Який порядок розв’язання задач за допомогою теореми про зміну кількості руху матеріальної системи?

9. Сформулюйте і запишіть теорему Ейлера для суцільних середовищ (для рідини).

10. Що називають секундною масою?

11. Які сили називають об’ємними? Наведіть приклади.

12. Які сили називають поверхневими? Наведіть приклади таких сил.

13. Сформулюйте план розв’язання задач з використанням теореми Ейлера для рідини.

14. Запишіть теорему Ейлера в проекціях на вісі декартових координат.

15. Яка сила називається реактивною?

16. З якої теореми можна одержати рівняння Мещерського?

17. Запишіть рівняння Мещерського.

18. Які є частинні випадки рівняння Мещерського і до рівнянь яких фізичних законів вони зводяться?

19. В чому полягають задачі Ціолковського?

20. Запишіть формулу Ціолковського для тіла змінної маси.

21. Яку величину називають ефективною швидкістю витікання?

22. Яким рівнянням описується рух ракети?

23. Як записати рівняння руху ракети при відсутності атмосфери?

24. Як інтерпретується формула Ціолковського при відсутності сили тяжіння і опору атмосфери?

25. Яке число називають числом Ціолковського? Що воно показує?