Теорема про змiну моменту кiлькостi руху матерiальної системи

Повна похiдна за часом від вектора момента кiлькостi руху матерiальної системи вiдносно нерухомого центру О дорiвнює сумi моментiв всiх зовнiшнiх сил вiдносно того ж центру:

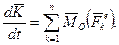(13.22)

Моментом кiлькостi руху (кiнетичним моментом) матерiальної системи вiдносно центру О називається сума моментiв кiлькостей руху всiх матерiальних точок, що входять до складу системи, вiдносно того ж центра :

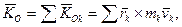(13.23)

де 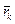- радiус-вектор матерiальної точки маси m_k з початком в центрi О; m_k - маса k-тої точки; 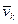- швидкiсть k-тої матерiальної точки. Якщо матерiальна система являє собою безперервно розподiлене матерiальне середовище, що заповнює деякий об’єм, то сума перейде у вiдповiдний iнтеграл.

В проекцiях на нерухомi осi декартових координат, початок яких спiвпадає з центром О, векторне рiвняння (13.22) еквiвалентне трьом скалярним:

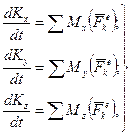(13.24)

де K_x, K_y, K_z – проекції вектора 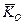на координатнi вiсi з початком в центрi О, якi можна визначити за формулами:

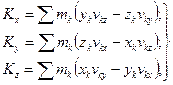(13.25)

де x_k, y_k, z_k - координати точки маси m_k.

Момент кiлькостi руху твердого тiла при обертаннi навколо нерухомої осi дорiвнює добутку моменту iнерцiї тiла вiдносно цiєї ж осi та проекцiї кутової швидкостi тiла на цю вiсь:

K_z = I_zω_z. (13.26)

У випадку сферичного руху твердого тiла

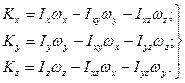(13.27)

Якщо осi координат, що мають початок в нерухомiй точцi О тiла, будуть головними осями iнерцiї, то

I_xy = I_xz = I_yz = 0

i з (13.27) одержимо

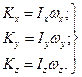(13.28)

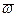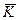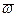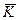Формули (13.28) визначають проекцiї моменту кiлькостi руху твердого тiла, що має одну нерухому точку, на осi координат, незмiнно пов’язанi з тiлом. З цих формул видно, що в загальному випадку проекцiї вектора i проекцiї вектора не пропорцiйнi мiж собою, а тому напрям векторiв i не спiвпадає.

При русi тiла навколо нерухомої осi за умови, що вона спiвпадає з вiссю обертання тiла, маємо

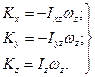(13.29)

Якщо матерiальна система здiйснює складний рух, то момент кiлькостi абсолютного руху 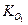вiдносно нерухомого центра О₁ дорiвнює сумi моменту кiлькостi руху центра мас системи вiдносно О₁ в припущеннi, що в ньому зосереджена вся маса системи, i моменту кiлькостi вiдносного руху вiдносно центра мас:

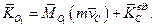(13.30)

В проекцiях на декартовi осi координат

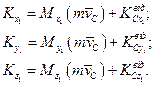(13.31)

Теорема про змiну кiнетичного моменту матерiальної системи має такi наслiдки:

а) внутрiшнi сили безпосередньо не впливають на змiну моменту кiлькостi руху матерiальної системи. Внутрiшнi сили можуть мати вплив на рух системи через зовнiшнi сили;

б) якщо головний момент всiх зовнiшнiх сил вiдносно деякого нерухомого центру дорiвнює нулю, то момент кiлькостi руху матерiальної системи вiдносно того ж центру не змiнюється за модулем i напрямом:

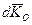( /dt) = 0, K_O = const;

в) якщо головний момент всiх зовнiшнiх сил вiдносно нерухомої осi (наприклад, осi х) дорiвнює нулю, то момент кiлькостi руху матерiальної системи не змiнюється в процесi руху:

(dК_x/dt) = 0, K_x = const.

При розв’язаннi задач з використанням теореми про змiну моменту кiлькостi руху матерiальної системи необхiдно дотримуватись такої послiдовностi:

1) вибрати координатнi осi, направити одну з осей вздовж нерухомої осi обертання;

2) показати на рисунку всi зовнiшнi сили системи;

3) записати теорему про змiну головного моменту кiлькостi руху матерiальної системи вiдносно вибраної осi, наприклад

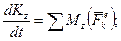
4) обчислити суму моментiв зовнiшнiх сил вiдносно осi z;

5) обчислити кiнетичний момент системи вiдносно нерухомої осi;

6) скласти рiвняння теореми про змiну кiнетичного моменту системи;

7) обчислити шуканi величини.

Зауваження. Для закріплення матеріалу §13 (пункт 13.6) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 37.1 - 37.5, 37.50, 37.52, 37.56;

2) № 37.6, 37.7, 39.9, 37.11, 37.43 – 37.48, 37.53;

3) № 37.57 - 37.59.

Рекомендується розв’язати також задачі № 9.18, 9.19, 9.21, 9.24 - 9.28, 9.38, 9.39, 9.43 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Сформулюйте теорему про зміну вектора моменту кількості руху матеріальної системи відносно нерухомого центра.

2. Що називають моментом кількості руху матеріальної системи відносно центра (або кінетичним моментом)?

3. Запишіть теорему про зміну кінетичного моменту в проекціях на осі декартових координат.

4. Як визначаються проекції вектора кінетичного моменту на нерухомі вісі декартових координат?

5. Як визначається момент кількості руху твердого тіла при його обертанні навколо нерухомої осі?

6. Як визначаються проекції кінетичного моменту на декартові вісі координат у випадку сферичного руху тіла?

7. Як записуються попередні рівняння, якщо вісі координат будуть головними осями інерції тіла?

8. Як пов’язані між собою напрями вектора кутової швидкості тіла і вектора його кінетичного моменту?

9. За якими формулами визначаються проекції кінетичного моменту тіла при його обертанні навколо нерухомої осі?

10. Як визначається момент кількості абсолютного руху матеріальної системи у випадку її складного руху?

11. Запишіть рівняння, яке визначає момент кількості абсолютного руху системи в проекціях на вісі декартових координат.

12. Які наслідки випливають з теореми про зміну кінетичного моменту матеріальної системи?

13. Сформулюйте послідовність розв’язування задач з використанням теореми про зміну кінетичного моменту системи.

13. 7. Теорема про зміну кінетичної енергіїматеріальної системи

Зміна кінетичної енергії матеріальної системи при її переході з початкового в кінцеве положення дорівнює сумі робот всіх зовнішніх та внутрішніх сил, прикладених до точок системи, на цьому переміщенні:

Т- Т₀ = А^е + А^і, (13.32)

де Т₀- початкове значення кінетичної енергії, Т - кінцеве значення кінетичної енергії , А^е і А^і - роботи всіх зовнішніх і внутрішніх сил системи.

Продиференціюємо рівність (13.32) за часом:

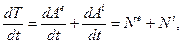(13.33)

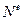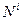де і - потужності зовнішніх і внутрішніх сил системи.

Рівність (13.33) є аналітичним записом теореми про зміну кінетичної енергії системи в диференціальній формі: повна похідна від кінетичної енергії за часом дорівнює сумі потужностей всіх зовнішніх і внутрішніх сил, прикладених до системи.

За допомогою теореми про зміну кінетичної енергії в інтегральній формі визначають:

1) швидкості точок матеріальної системи;

2) роботу однієї з сил, прикладених до системи, коли з умови задачі швидкості точок матеріальної системи відомі або їх можна визначити іншими методами.

Диференціальна форма теореми про зміну кінетичної енергії системи матеріальних точок застосовується для складання диференціальних рівнянь руху, а також для визначення лінійних або кутових прискорень.

Кінетична енергія матеріальної системи дорівнює сумі кінетичних енергій всіх матеріальних точок:

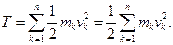(13.34)

Кінетична енергія твердого тіла обчислюється за формулами:

а) при поступальному русі

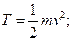(13.35)

б) при обертанні твердого тіла навколо нерухомої осі

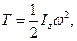(13.36)

де І_z - момент інерції твердого тіла відносно осі обертання z, ω - кутова швидкість обертання;

в) при плоскому русі

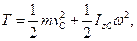(13.37)

де v_C - швидкість центра мас тіла, І_zC - момент інерції тіла відносно осі z, що проходить через центр мас перпендикулярно до площини руху, ω - величина миттєвої кутової швидкості твердого тіла. В цьому випадку обчислення кінетичної енергії можна робити також за формулою

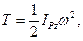(13.38)

де І_Pz - момент інерції твердого тіла відносно осі z, що проходить через миттєвий центр швидкостей перпендикулярно до площини руху;

г) при обертанні навколо нерухомої точки (при сферичному русі)

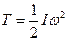, (13.39)

де І - момент інерції тіла відносно миттєвої осі обертання, ω - модуль миттєвої кутової швидкості.

Якщо вибрати початок рухомих осей х, у, z, пов’язаних з твердим тілом, в нерухомій точці О, то

(13.40)

Якщо х, у, z є головними осями інерції твердого тіла в нерухомій точці О, то І_ху=І_xz=І_yz=0, і значить

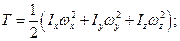(13.41)

д) в загальному випадку руху твердого тіла

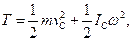(13.42)

де v_C - модуль швидкості центра мас, І_C - момент інерції відносно миттєвої осі, що проходить через центр мас, ω - модуль миттєвої кутової швидкості.

Якщо вибрати початок рухомих координатних осей х, у, z в центрі мас, то

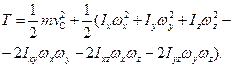(13.43)

Якщо осі х, у, z є головними центральними осями інерції в центрі мас С, то І_ху=І_xz=І_yz=0, і значить

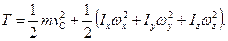(13.44)

Теорема Кеніга: кінетична енергія механічної системи при довільному русі дорівнює сумі кінетичної енергії центра мас в припущенні, що в ньому зосереджена маса всієї системи, і кінетичної енергії системи в її русі по відношенню до центра мас:

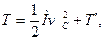(13.45)

де 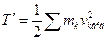- кінетична енергія системи в її русі відносно центру мас, v_kвід - швидкість k-тої точки системи по відношенню до рухомих осей координат.

Розв’язання задачі за допомогою теореми про зміну кінетичної енергії можна проводити в такій послідовності:

1) показати на рисунку всі зовнішні і внутрішні сили системи. Якщо система незмінювана, то треба показувати тільки зовнішні сили;

2) обчислити суму робот всіх зовнішніх і внутрішніх сил на переміщеннях точок системи. Якщо система незмінювана, то потрібно обчислити тільки роботу зовнішніх сил;

3) обчислити кінетичну енергію системи в початковому і кінцевому положеннях системи;

4) записати теорему про зміну кінетичної енергії системи матеріальних точок:

,

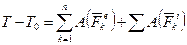для незмінюваної системи ;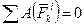

5) визначити шукану величину.

Зауваження. Для закріплення матеріалу §13 (пункт 13.7) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 38.1, 38.3, 38.4, 38.7 - 38.10, 38.11, 38.13, 38.14, 38.20, 38.21, 38.27;

2) № 38.16 - 38.18, 38.23, 38.24, 38.27, 38.28, 38.30 – 38.33, 38.35, 38.36, 38.38, 38.40, 38.44;

3) № 38.42, 38.43, 38.46, 38.47, 38.50, 38.51 - 38.53.

Рекомендується розв’язати також задачі № 9.46, 9.47, 9.49, 9.50, 9.52, 9.53, 9.55, 9.57 – 9.59, 9.63 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Сформулюйте теорему про зміну кінетичної енергії матеріальної системи.

2. Запишіть і сформулюйте теорему про зміну кінетичної енергії в диференціальній формі.

3. Що можна визначити за допомогою теореми про зміну кінетичної енергії системи, записаної в інтегральній формі?

4. Для чого застосовують теорему про зміну кінетичної енергії системи в диференціальній формі?

5. Як визначити кінетичну енергію матеріальної системи?

6. Як обчислити кінетичну енергію твердого тіла у випадку його поступального руху та при його обертанні навколо нерухомої осі?

7. За якою формулою обчислюють кінетичну енергію твердого тіла у випадку його плоского руху?

8. Як можна обчислити кінетичну енергію при сферичному русі тіла?

9. Як обчислюють кінетичну енергію в загальному випадку руху твердого тіла?

10. Сформулюйте і запишіть теорему Кеніга.

11. Яка послідовність розв’язування задач за допомогою теореми про зміну кінетичної енергії матеріальної системи?