Теорема про змiну кiлькостi руху матерiальної системи

Похiдна за часом вiд вектора кiлькостi руху системи матерiальних точок дорiвнює головному вектору всiх зовнiшнiх сил, дiючих на систему:

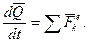(13.6)

Кiлькiстю руху матерiальної системи називається вектор 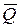, рiвний сумi кiлькостей руху матерiальних точок, що входять в систему:

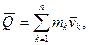(13.7)

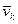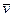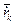де m_k - маса k-тої матерiальної точки, - її швидкiсть. Через те, що _k = , де 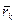– радiус-вектор k-тої точки, проведений з початку iнерцiальної системи вiдлiку, то з (13.7) маємо:

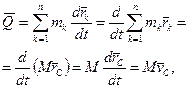(13.8)

де 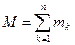- маса матерiальної системи, 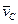– швидкiсть центра мас. З формули (13.8) зробимо висновок: кiлькiсть руху матерiальної системи дорівнює добутку маси всiєї системи та швидкості її центра мас. В проекцiях на нерухомi осi декартових координат векторне рiвняння (13.6) еквiвалентне трьом скалярним:

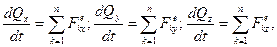(13.9)

де

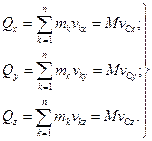(13.10)

Ця теорема має декiлька наслiдкiв:

а) внутрiшнi сили безпосередньо не впливають на змiну кiлькостi руху матерiальної системи – вони можуть впливати на рух через зовнiшнi сили;

б) якщо головний вектор всiх зовнiшнiх сил, дiючих на систему, дорiвнює нулю, то вектор кiлькостi руху матерiальної системи залишається постiйним за величиною i напрямком:

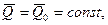
де 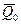– початкове значення вектора ;

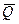в) якщо проекцiя головного вектора всiх зовнiшнiх сил, прикладених до системи, на будь-яку нерухому вiсь дорiвнює нулю, то проекцiя кiлькостi руху матерiальної системи на цю вісь залишається постiйною:

Q_x = Q_0x = const,

де Q_0x - початкове значення проекцiї Q_x.

Рiвнiсть (13.6) можна записати i так:

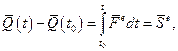(13.11)

де 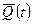– кiлькiсть руху матерiальної системи в момент часу t, 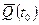- кiлькiсть руху матерiальної системи в момент часу t₀,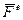 – головний вектор зовнiшнiх сил, 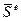= Σ 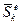– головний вектор iмпульсiв зовнiшнiх сил.

Рiвнiсть (13.11) виражає теорему про змiну кiлькостi руху матерiальної системи в iнтегральнiй формi:

змiна кiлькостi руху матерiальної системи за промiжок часу [t₀, t] дорiвнює головному вектору iмпульсiв всiх зовнiшнiх сил, прикладених до системи, за той же промiжок часу.

Векторне рiвняння (13.11) еквiвалентне трьом скалярним рiвнянням:

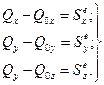(13.12)

де S_x^e, S_y^e i S_z^e - проекцiї головного вектора iмпульсiв всiх зовнiшнiх сил на осi координат; Q_x, Q_y, Q_z i Q_0x, Q_0y, Q_0z – значення проекцiй кiлькостi руху матерiальної системи в моменти часу t i t₀ відповідно.

Теорему про змiну кiлькостi руху матерiальної системи в формi (13.11) або (13.12) широко застосовують в теорiї удару.

При розв’язаннi задач за допомогою теореми про змiну кiлькостi руху матерiальної системи корисно дотримуватись такого порядку:

1) показати на рисунку всi зовнiшнi сили;

2) вибрати систему координат;

3) записати теорему про змiну головного вектора кiлькостi руху в проекцiях на осi координат;

4) з одержаних рiвнянь визначити шуканi величини.

Теорема Ейлера

Сума головних векторiв об’ємних i поверхневих сил, а також векторiв секундних кiлькостей руху рiдини, яка протiкає через два перерiзи труби, дорiвнює нулю, якщо вектори секундних кiлькостей руху направленi у середину видiленого перерiзами об’єму:

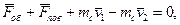(13.13)

де m_c = ρ₁v₁S₁ = ρ₂v₂S₂ - секундна маса - маса рiдини, що протiкає за одиницю часу через перерiз площею S₁ або S₂;

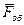-головний вектор об’ємних сил. Об’ємними називаються сили, якi дiють на всi частинки рiдини, розташованi як у серединi, так i на поверхнi розглянутого об’єму (наприклад, сили ваги частинок рiдини);

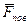-головний вектор поверхневих сил. Поверхневими силами називаються сили, якi дiють на частинки рiдини, розташованi на зовнiшнiй поверхнi об’єма (наприклад, реакцiї стiнок труби);

ρ - густина рiдини.

При користуваннi теоремою Ейлера потрiбно:

1) показати на рисунку об’ємнi i поверхневi сили;

2) показати на рисунку вектори секундних кiлькостей руху рiдини (або газу), протiкаючої через два перерiзи, що обмежують розглядуваний об’єм рідини, при цьому вектори секундних кiлькостей руху треба направити всередину цього об’єму;

3) вибрати систему координат;

4) записати теорему Ейлера в проекцiях на осi декартових координат:

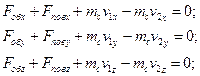(13.14)

5) визначити шуканi величини.