Загальнi теореми динамiки матерiальної точки

9. 1. Теорема про змiну кiлькостi руху (iмпульсу) точки. Методичнi вказiвки до розв’язання задач

Кількістю руху (імпульсом) матерiальної точки називають добуток маси точки та її швидкості:

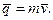(9.1)

За другим законом Ньютона маємо

d(m 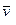) = 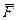·dt. (9.2)

Лiва частина формули (9.2) - геометрична змiна iмпульсу рухомої матерiальної точки за нескiнченно малий промiжок часу dt. У правiй частинi цiєї формули - добуток дiючої сили та нескiнченно малого промiжку часу її дiї:

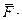dt = d 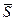. (9.3)

Це є елементарний iмпульс прикладеної сили. З (9.2) видно, що елементарний iмпульс прикладеної сили характеризує ту кiлькiсть руху, яка надходить вiд навколишнiх тiл до точки за нескiнченно малий промiжок часу.

Рiвняння (9.2) виражає теорему:

геометрична змiна кiлькостi руху (iмпульсу) матерiальної точки за нескiнченно малий промiжок часу дорiвнює елементарному iмпульсу прикладеної сили за той же промiжок часу.

При iнтегруваннi (9.2) одержимо:

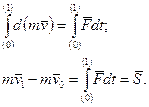(9.4)

Початкове положення матерiальної точки тут позначене значком (0), кiнцеве положення - (1).

Величина 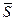називається iмпульсом сили за даний скiнченний промiжок часу.

Рiвняння (9.4) виражає теорему:

геометричний прирiст кiлькостi руху (iмпульсу) рухомої матерiальної точки за скiнченний промiжок часу дорiвнює iмпульсу прикладеної сили за той же самий промiжок часу.

У проекцiях на осi декартової системи координат рiвняння (9.4) запишеться так:

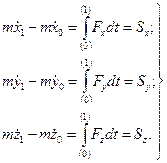(9.5)

Тобто, прирiст проекцiї вектора кiлькостi руху (iмпульсу) на кожну нерухому координатну вiсь дорiвнює проекцiї iмпульсу прикладеної сили за той же самий промiжок часу i на ту ж вiсь.

У випадку, коли 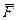= 0, з (9.2) витiкає, що m 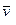= const. Це закон збереження iмпульсу матерiальної точки: якщо рiвнодiйна прикладених до матерiальної точки сил дорiвнює нулю, то iмпульс матерiальної точки зберiгається незмiнним за величиною i за напрямом.

При розв’язуваннi задач на застосування теореми про змiну кiлькостi руху матерiальної точки доцiльно дотримуватися таких методичних вказiвок:

1) вибрати об’єкт дослiдження, прийняти його за матерiальну точку, показати цю точку в довiльний момент часу (в промiжному положеннi), показати вектори швидкостей в початковий i кiнцевий моменти часу;

2) прикласти всi активнi (заданi) сили;

3) вiдкинути в’язi, замiнивши їх реакцiями;

4) вибрати систему координат;

5) скласти теорему про змiну кiлькостi руху в проекцiях на осi координат;

6) виразити всi члени, що входять в усi рiвняння, через вiдомi i шуканi величини;

7) розв’язати цi рiвняння вiдносно шуканих величин.

Зауваження. Для закріплення матеріалу §9 (пункт 9.1) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 28.1, 28.2, 28.6;

2) № 28.5, 28.8, 28.12;

3) № 28.16, 28.17, 28.18, 28.20.

Питання для самоконтролю

1. Що називають імпульсом матеріальної точки?

2. Запишіть другий закон Ньютона, використовуючи поняття імпульсу матеріальної точки.

3. Що називається елементарним імпульсом прикладеної сили та що він характеризує?

4. Сформулюйте теорему про зміну кількості руху матеріальної точки за нескінченно малий проміжок часу.

5. Запишіть математичний вираз і сформулюйте теорему про геометричний приріст кількості руху матеріальної точки за скінчений проміжок часу.

6. Яку величину називають імпульсом сили за заданий скінчений проміжок часу?

7. Як записується та як формулюється теорема про зміну кількості руху матеріальної точки в проекціях на осі декартової системи координат?

8. Сформулюйте закон збереження імпульсу матеріальної точки.