Дослiдження руху невiльної матерiальної точки в осях натурального тригранника

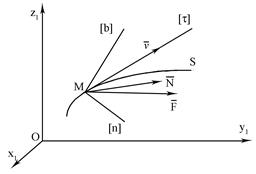
Розглянемо рух матерiальної точки маси m по заданiй нерухомiй iдеально гладенькiй поверхнi під дією активних сил (рис. 7.2). Прикладом такого руху може бути рух кульки в криволiнiйнiй трубцi. Рух цiєї невiльної матерiальної точки в векторнiй формi запишеться у виглядi рiвняння (7.4). В проекцiї на осi натурального тригранника - дотичну τ, головну нормаль n i бiнормаль b до кривої S – одержимо:

Рис. 7. 2.

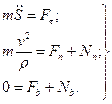(7.13)

В цьому випадку реакцiя в’язi 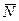перпендикулярна до заданої кривої, тобто розташована в площинi Mbn.

Рiвняння (7.13) називаються диференцiальними рiвняннями криволiнiйного руху невiльної матерiальної точки в проекцiях на осi натурального тригранника або рiвняннями у формi Ейлера.

Друге рiвняння системи рiвнянь (7.13) показує, що реакцiя в’язi при русi (динамiчна реакцiя) залежить не тiльки вiд вигляду в’язi i прикладених активних сил, як в статицi, але й вiд швидкостi руху.

Рiвняння (7.13) бiльш зручнi за рiвняння (7.10) i (7.12), бо вони дозволяють розв’язувати задачi про визначення закону руху точки i реакцiї в’язi незалежно одна вiд одної. Дiйсно, перше рiвняння не включає невiдому реакцiю i дозволяє визначити шляхом iнтегрування швидкiсть точки i закон руху точки вздовж заданої кривої, тобто S = S(t); два iнших рiвняння дозволяють знайти складовi реакцiї N_n i N_b. Але рiвняння в декартових координатах можна одержати i без припущення про стацiонарнiсть в’язi, тому вони є бiльш загальними.

Якщо рух матерiальної точки вiдбувається по заданiй iдеально гладенькiй кривiй i на матерiальну точку дiє активна сила 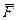, що лежить з цiєю кривою в однiй площинi, то реакцiя в’язi направлена по нормалi до кривої i лежить з нею в однiй площинi. В цьому разi рiвняння (7.13) набувають вигляду:

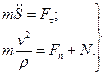(7.14)

Рiвняння в формi Ейлера можна використати i в тому випадку, коли матерiальна точка рухається по заданiй нерухомiй шершавiй кривiй. При цьому необхiдно добавити проекцiю сили тертя F_{τ теp} = μN.

Зауваження. Для закріплення матеріалу §7 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 31.1, 31.3, 31.4, 31.5, 31.6;

2) № 31.9, 31.10, 31.12, 31.13, 31.14, 31.16, 31.20, 31.22, 31.23, 31.24, 31.25;

3) № 31.17, 31.28, 31.29, 31.30, 31.33, 31.34.

Рекомендується розв’язати також задачі № 8.51, 8.54, 8.58, 8.59, 8.60 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Яку матеріальну точку називають невільною?

2. Що називають в’язями? Які рівняння називають рівняннями в’язі?

3. Яку в’язь називають гладенькою (ідеальною) та який напрям має реакція такої в’язі?

4. Як визначається реакція шершавої в’язі?

5. Як, згідно з законом Кулона, визначається динамічна сила тертя і який напрям вона має?

6. Сформулюйте аксіому в’язей.

7. Запишіть основний закон динаміки невільної матеріальної точки у векторній формі.

8. Якого вигляду набуває основний закон динаміки у випадку ідеальної поверхні?

9. Сформулюйте основну задачу динаміки невільної матеріальної точки.

10. Яку в’язь називають голономною? Запишіть загальний вигляд рівняння такої в’язі.

11. Які обмеження накладає голономна в’язь на напрям швидкості точки?

12. Дайте формулювання утримуючої та стаціонарної (склерономної) голономної в’язі.

13. Як записується диференціальне рівняння руху в векторній формі для матеріальної точки, що рухається по ідеальній поверхні?

14. Що називають градієнтом скалярної функції?

15. Як нормальна реакція виражається через градієнт функції ?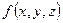

16. Як записуються диференціальні рівняння руху матеріальної точки по ідеально гладенькій поверхні в проекціях на осі декартової системи координат?

17. Які рівняння називають рівняннями Лагранжа першого роду?

18. З якої системи рівнянь можна визначити невідомі функції x, y, z i λ?

19. За якою формулою визначається модуль нормальної сили реакції?

20. Запишіть рівняння Лагранжа першого роду у випадку стаціонарної утримуючої голономної реальної в’язі.

21. Як можна представити проекції сили тертя на вісі декартових координат?

22. Яка система рівнянь дає можливість визначити невідомі величини у випадку реальної в’язі?

23. Запишіть диференціальні рівняння криволінійного руху матеріальної точки в проекціях на осі натурального тригранника. Як інакше називають ці рівняння?

24. Як розташована реакція 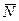в’язі відносно осей натурального тригранника?

25. Що показує рівняння проекцій на головну нормаль?

26. Які переваги рівнянь у формі Ейлера порівняно з рівняннями Лагранжа першого роду і навпаки?

27. Якого вигляду набувають рівняння руху невільної матеріальної точки, якщо вона рухається по гладенькій кривій?

28. Як записуються рівняння руху невільної матеріальної точки у формі Ейлера, якщо точка рухається по нерухомій шершавій кривій?

§8. Диференцiальнi рiвняння вiдносного руху матерiальної точки