Робота сил, прикладених до матерiальної точки i матерiальної системи. Потужнiсть

Робота - фiзична величина А, яка є кiлькiсною мiрою перетворення механiчного руху в iншi форми руху матерiї (теплоту, електрику i т. iн.).

Робота постiйної за модулем i напрямком сили на прямолiнiйному перемiщеннi дорiвнює скалярному добутку вектора сили 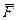та вектора перемiщення :

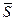A = 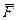· 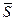= F·S·cosα, (9.6)

де α - кут мiж напрямком сили 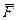i перемiщенням .

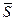В формулі (9.6) модулi сили F i перемiщення S завжди додатнi. Знак ”+” чи ”-” роботи А визначається знаком косинуса кута α або косинуса кута мiж напрямком сили 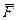i швидкостi .

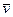Якщо напрям сили 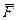спiвпадає з напрямом перемiщення 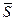, то кут (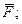 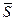) = ( 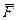; 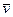) = α = 0°, cosα = 1i A = F·S.

Якщо α = 180° (сила направлена протилежно перемiщенню), то cosα = -1 i A = - F·S.

Якщо α = 90° (сила перпендикулярна перемiщенню), то cosα= 0i А = 0.

Елементарною роботою сили називають роботу на достатньо малому перемiщеннi точки її прикладання, при якому змiною сили можна нехтувати:

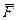
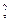
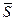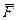
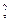
δA = Fcosα·dS = Fcos( )dS = Fcos( 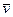)dS. (9.7)

Термiн ”робота” в науку було введено Г. Корiолiсом i одночасно Ж. – В. Понселе.

В Мiжнароднiй системi одиниць (СI) робота вимiрюється в Джоулях (Дж). Робота в 1Дж - це робота сили в 1Н на шляху 1м, який збiгається з напрямом сили.

Теорема про елементарну роботу рiвнодiйної:

елементарна робота рiвнодiйної дорiвнює сумi елементарних робот складових сил

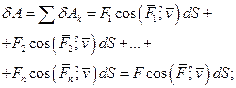(9.8)

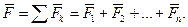
Визначення елементарної роботи через проекцiї сили на осi координат. Елементарна робота сили пов’язана з проекцiями сили на осi декартових координат спiввiдношенням:

δA = F_xdx+F_ydy+F_zdz = Xdx+Ydy+Zdz. (9.9)

В формулi (9.9) X, Y, Z (aбo F_x, F_y, F_z) - проекцiї сили на осi координат, якi визначаються не тiльки величиною, але i знаком. Величини dx, dy, dz є диференцiалами координат точки прикладання сили i можуть бути як додатними, так i вiд’ємними. В загальному випадку диференцiальний тричлен Xdx+Ydy+Zdz не є повним диференцiалом i δА не потрiбно розумiти як повний диференцiал вiд роботи А.

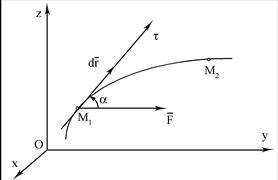
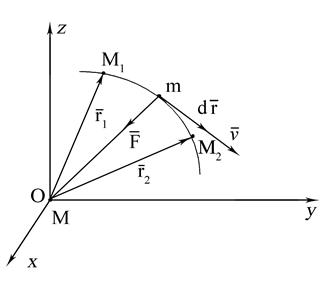
Робота змiнної сили на скiнченому перемiщеннi по криволiнiйнiй траєкторiї дорiвнює криволiнiйному iнтегралу вiд скалярного добутку векторiв сили 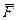i елементарного перемiщення 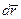, взятому вздовж дуги кривої вiд М₁ до М₂ (рис. 9.1).

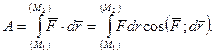(9.10)

Робота змiнної сили на скiнченному перемiщеннi по криволiнiйнiй траєкторiї визначається через проекцiї сили на осi декартових координат так:

(9.11)

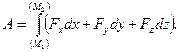Рис. 9. 1.

Робота сили ваги матерiальної точки з формули (9.11), оскiльки в цьому випадку F_x = F_y = 0, F_z = - G, дорiвнює добутку ваги матерiальної точки та рiзниці рiвнiв початкового i кiнцевого положень цiєї точки.

Робота сили ваги не залежить вiд форми траєкторiї рухомої матерiальної точки:

A₁₂ = mg(z₁ - z₂) = mgΔh. (9.12)

Якщо матерiальна точка наближається до земної поверхнi, то А( 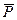)>0, а якщо вiддаляється, то А( 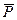)<0. Якщо висоти початкового i кiнцевого положень рiвнi (наприклад, рух матерiальної точки по замкненому контуру), то А( 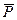) = 0.

Силова функцiя сили тяжiння має вигляд

U =- mgz. (9.13)

Робота сили всесвiтнього тяжiння (рис. 9.2) на скiнченому перемiщеннi матерiальної точки з положення М₁ в положення М₂ дорiвнює:

А₁₂ = γmМ[(1/r₂) - (1/r₁)]. (9.14)

Силова функцiя центральної сили тяжiння дорiвнює:

U = γmM(1/r). (9.15)

Рис. 9. 2.

Робота пружної сили 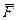_пр = - cx на прямолiнiйному перемiщеннi по лiнiї дiї сили з точки з абсцисою x₁ в точку з абсцисою х₂ дорiвнює:

А = - (с/2)( 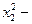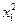) = (с/2)( 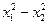). (9.16)

Силова функцiя пружної сили:

U = - (cx²/2). (9.17)

Робота пружної сили дорiвнює половинi добутку коефiцiєнта пружностi с та рiзниці квадратiв початкової i кiнцевої деформацiй пружини.

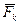
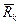Якщо система сил прикладена до механiчної системи, то її робота дорiвнює сумi робот всiх сил, якi можуть бути роздiленi на заданi i реакцiї в'язей або на зовнiшнi 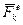i внутрішні :

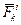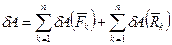(9.18)

або

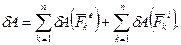(9.19)

Цi формули можна записати в проекцiях на координатнi осi:

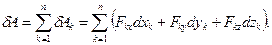(9.20)

Елементарна робота внутрiшнiх сил незмiнюваної системи матерiальних точок (наприклад, абсолютно твердого тiла) дорiвнює нулю:

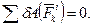(9.21)

В системi матерiальних точок, що змiнюється (наприклад, пружне тiло) робота внутрiшнiх сил не дорiвнює нулю.

У випадку системи матерiальних точок робота сили ваги дорiвнює добутку сили ваги всiєї системи та рiзниці висот кiнцевого i початкового положень центра мас системи:

A = - P(z_2C - z_1C), (9.22)

де 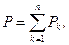вiсь z направлена вертикально вгору.

Елементарна робота сил, прикладених до твердого тiла, обчислюється за такими формулами:

а) при поступальному русi:

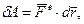(9.23)

де 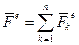- головний вектор системи зовнiшнiх сил, 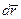- елементарне перемiщення будь-якої з точок твердого тiла ( або його центра мас - );

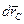б) при обертаннi навколо нерухомої осi:

δA = M_z^e ×dφ, (9.24)

де M_z^e - головний момент системи зовнiшнiх сил вiдносно осi обертання z, dφ - елементарне кутове перемiщення твердого тiла;

в) при плоскому русi:

δA = 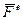· 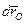+ M_zO^e·dφ, (9.25)

де 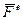- головний вектор системи зовнiшнiх сил, 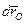- елементарне перемiщення полюса О, M_zO^e - головний момент системи зовнiшнiх сил вiдносно осi z, яка проходить через полюс О перпендикулярно до площини руху, dφ - елементарне кутове перемiщення тiла навколо осi z. Полюс вибирається довiльно.

Потужнiсть N характеризує швидкiсть здiйснення роботи протягом певного часу. Вона визначається формулою:

N = dA/dt. (9.26)

Якщо сила 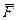прикладена до матерiальної точки або до абсолютно твердого тiла, що здiйснює поступальний рух, то потужнiсть сили 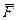дорiвнює

N = F×v, (9.27)

де v - швидкiсть матерiальної точки (твердого тiла).

Якщо момент М_z прикладений до твердого тiла, що обертається навколо нерухомої осi z з кутовою швидкiстю ω, то потужнiсть моменту дорiвнює:

N = M_zω = M_z(dφ/dt). (9.28)

Одиниця вимiрювання потужностi в системi СI – Ватт:

1Вт = 1Дж/с.

Обчислення суми робот сил, прикладених до матерiальної точки або до системи матерiальних точок, можна виконувати в такiй послiдовностi:

1) показати на рисунку сили, якi прикладенi до матерiальної точки або системи точок;

2) показати елементарнi перемiщення точок системи;

3) обчислити елементарну роботу сил, тобто суму робот всiх сил на елементарних перемiщеннях точок системи;

4) обчислити суму робот на скiнчених перемiщеннях.