Рiвняння руху вiльної матерiальної точки вiдносно Землi

Запишемо рiвняння руху матерiальної точки вiдносно Землi, користуючись поняттям ваги:

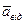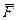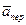m = - m - 2m( 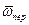´ 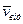), (8.17)

або, враховуючи, що 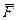- m 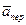= 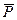, одержимо

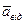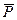m = -2m( ´ ).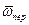

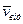Замiнюючи вагу 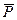через m i скорочуючи на m, запишемо остаточно:

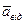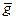= - 2( 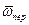´ 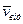). (8.18)

Це рiвняння руху вiльної матерiальної точки вiдносно Землi.

Маятник Фуко

Добове обертання Землi навколо своєї осi можна виявити, спостерiгаючи за коливанням тягаря, пiдвiшеного на довгiй нитцi. Цей дослiд уперше здiйснив у 1851 роцi французький фiзик Ж.-Б.-Л.Фуко, який скористався маятником довжиною 67 м з тягарем на кiнцi нитки, який важив 30 кг.

Розглянемо математичну теорiю маятника. Систему вiдлiку вибираємо так: вiсь Oz направимо вертикально вгору, вiсь Oy - по дотичнiй до паралелi на схiд, i вiсь Ох - у площинi меридiана (рис. 8.4). Початок координат O збiгається з точкою пiдвiсу маятника.

Реакцiю 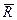нитки можна подати у виглядi

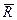= R(- 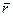/l), (8.19)

де 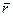- радiус-вектор тягаря маятника, l - довжина нитки, (- 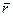/l) - одиничний вектор, що визначає напрям реакцiї нитки. З рiвнянь (8.18) i (8.19) знайдемо

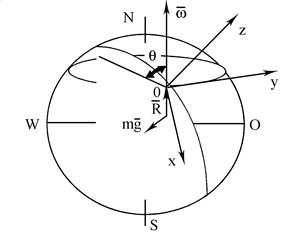
Рис. 8. 4.

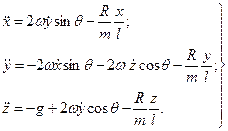(8.20)

Тут враховано, що ω_x = - ωcosθ, ω_у = 0, ω_z = ωsinθ.

Розглянемо малi коливання маятника. Координати тягаря задовольняють рiвнянню сфери:

x² + y² + z² - l²= 0,

тодi

z/l = - [1 - (( x²+y²)/l²)]^1/2 = - [1 - (( x²+y²)/2l²)+...] ≈ - 1,

тобто z = - l з точнiстю до величин другого порядку малостi, величинами dz/dt i d²z/dt² можна знехтувати як величинами другого порядку малостi.

Пiсля спрощення рiвняння (8.20) можна записати так:

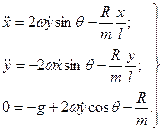(8.21)

З третього рiвняння знайдемо R, нехтуючи доданком 2ω 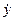cosθ (величина 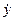/l за умовою є малою величиною). Отже, маємо

R ≈ mg. (8.22)

Це означає, що натяг нитки маятника залишається приблизно сталим i дорiвнює вазi тягаря, який коливається. З (8.21) при цiй умовi знайдемо

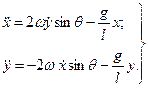(8.23)

Цю систему рiвнянь проiнтегруємо так. Помножимо друге рiвняння на 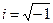i додамо до першого рiвняння. Позначимо х+iу = U. Одержимо лiнiйне рiвняння

(d²U/dt²) + 2ω₁(dU/dt)I + n²U = 0, (8.24)

де n² = g/l; ωsinθ = ω₁.

Шукаємо розв'язок рiвняння (8.24) у формi

U = e^λt.

Характеристичне рiвняння

λ² + 2ω₁λi + n² = 0;

його коренi такi:

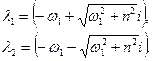
Позначимо 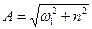, тодi

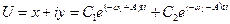, (8.25)

де C₁i C₂ - довiльнi сталi.

Розглянемо рух, при якому C₁ = - C₂ = c . Тодi маємо

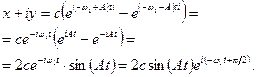(8.26)

Абсолютна величина цього комплексного виразу дорiвнює

|x + iy| = 2csin(At), (8.27)

а аргумент

α = π/2 - ω₁t. (8.28)

Формули (8.27) i (8.28) показують, що точка М (проекцiя тягаря маятника на горизонтальну площину xOy) коливається гармонiчно вздовж прямої, яка проходить через початок координат, а сама ця пряма рiвномiрно обертається з кутовою швидкiстю

da/dt = -ω₁ = -ωsinθ.

Знак ”мінус” тут означає, що обертання вiдбувається за стрiлкою годинника (зi сходу через пiвдень на захiд), якщо дивитися зверху (рис. 8.5).

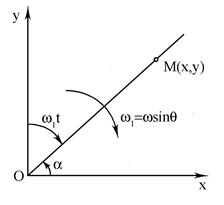
Рис. 8.5

Встановимо початковi умови такого руху. Знайдемо похiдну за часом вiд величини U:

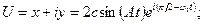
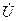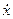= + i 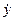= [2Accos(At) +2c(π/2-ω₁t)isin(At)] 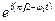.(8.29)

При t₀= 0 х₀ + iу₀= 0; 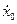+ i 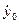= 2cАе^iπ/2,

звiдки х₀= =0; у₀ 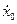= 0; = 0; 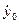= 2сА ≠ 0.

Це значить, що маятник у початковий момент часу одержав поштовх у положеннi рiвноваги в напрямi на схiд або на захiд.

Рис. 8. 5.

Таким чином, якщо маятнику надати поштовху в станi рiвноваги в напрямi на схiд або на захiд, то вiн гармонiчно коливається по вiдрiзку прямої, яка проходить через положення рiвноваги маятника. Ця пряма обертається рiвномiрно навколо вертикалi з кутовою швидкiстю ω₁ = ωsinθ. Все це i є доказом обертання Землi.

Зауваження. Для закріплення матеріалу §8 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 33.1, 33.2, 33.3, 33.5, 33.16;

2) № 33.4, 33.7, 33.9, 33.13, 33.14, 33.18, 33.19;

3) № 33.20, 33.21, 33.22.

Рекомендується розв’язати також задачі № 8.24, 8.25, 8.28, 8.29, 8.34, 8.39, 8.40, 8.41, 8.42, 8.44 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Який рух матеріальної точки називають абсолютним і який - відносним?

2. В чому полягає основна задача динаміки відносного руху матеріальної точки?

3. Сформулюйте порядок розв’язання задачі відносного руху матеріальної точки.

4. Виведіть і запишіть рівняння відносного руху матеріальної точки.

5. Яка сила називається переносною силою інерції і яка сила – коріолісовою силою інерції?

6. Запишіть основний закон динаміки в векторній формі для відносного руху невільної матеріальної точки.

7. Як в загальному випадку визначаються переносне прискорення і коріолісове прискорення?

8. Як можна скласти основне рівняння динаміки відносного руху, використовуючи основне рівняння динаміки абсолютного руху матеріальної точки?

9. Як записується рівняння відносного руху матеріальної точки в проекціях на осі системи відліку Оxyz?

10. Які сили діють на тягар, підвішений до нитки біля поверхні Землі?

11. Який рух виконує тягар на нитці завдяки добовому обертанню Землі? Яка сила діє на тягар в цьому випадку і як вона визначається ?

12. Що називається вертикаллю і географічною широтою місця?

13. Запишіть основне рівняння відносного спокою тягаря.

14. За яких умов можливий відносний рух тягаря на нитці?

15. Чому дорівнює геометрична сума сил у випадку відносного спокою матеріальної точки?

16. Як визначається вага тіла?

17. Поясніть особливості вимірювання ваги тіла на пружинних терезах.

18. Чому дорівнює вага тіла згідно з її означенням?

19. Які значення має сила ваги на полюсі і на екваторі?

20. Як за другим законом Ньютона визначається сила притягання тіла до землі?

21. Як визначити прискорення g і абсолютне прискорення g₀?

22. Яке нормальне значення g_н, прийняте в Міжнародній системі одиниць СІ?

23. Запишіть рівняння руху матеріальної точки відносно Землі, використовуючи поняття ваги.

24. Який вигляд має рівняння руху вільної матеріальної точки відносно Землі?

25. Який дослід з маятником здійснив французький вчений – фізик Ж.-Б.-Л. Фуко?

26. Чому дорівнює натяг нитки маятника, який виконує малі коливання?

27. Як рухається точка М, що є проекцією тягаря маятника на площину xОy?

28. Що означає знак „мінус” в рівнянні обертання прямої, вздовж якої проходять коливання точки М?

29. Що означають початкові умови в досліджені руху маятника Фуко?

30. Які висновки можна зробити з дослідів, проведених з маятником Фуко?