Дослiдження руху невiльної матерiальної точки в декартових координатах
Якщо накладенi на матерiальну точку в’язi обмежують тiльки вiльнiсть її перемiщення в просторi, не накладаючи обмежень на модуль її швидкостi, то така в’язь називається голономною або геометричною. Рiвняння голономної в’язi записується так:
f(x, y, z) = 0. (7.5)
Координати матерiальної точки задовольняють рiвнянням (7.5) пiд час руху, доки точка залишається на поверхнi. Крiм того, голономна в’язь типу, описаного рівнянням (7.5), накладає обмеження на напрям швидкостi рухомої точки. Це обмеження заключається в тому, що вектор швидкостi точки лежить завжди в площинi, дотичній до поверхнi.
Якщо накладена на матерiальну точку голономна в’язь така, що точка залишається на поверхнi, то ця в’язь називається утримуючою. Математично рiвняння такої в’язi записується у формi рiвностi (7.5).
Якщо рiвняння накладеної на матерiальну точку голономної в’язi не мiстить явно часу, тобто записується у формi рiвностi (7.5), то це значить, що поверхня, по якiй рухається матерiальна точка, нерухома i не деформується. Така голономна в’язь називається стацiонарною або склерономною.
|
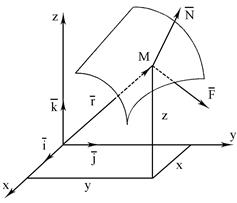 Розглянемо рух точки М маси m по поверхнi (рис. 7.1). Будемо вважати, що в’язь, накладена на матерiальну точку, є стацiонарною утримуючою i голономною. Крiм того, ця в’язь є iдеальною (без тертя). Ось чому для цiєї матерiальної точки диференцiальне рiвняння руху в векторнiй формi можна записати так:
Розглянемо рух точки М маси m по поверхнi (рис. 7.1). Будемо вважати, що в’язь, накладена на матерiальну точку, є стацiонарною утримуючою i голономною. Крiм того, ця в’язь є iдеальною (без тертя). Ось чому для цiєї матерiальної точки диференцiальне рiвняння руху в векторнiй формi можна записати так:
m 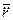 =
= 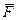 +
+ 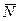 . (7.6)
. (7.6)
Рiвняння в’язi записується у формi (7.5). З курсу диференцiальної геометри вiдомо, що напрям зовнiшньої нормалi до поверхнi f(x, y, z)= 0 спiвпадає з напрямом вектора
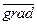 f =
f = 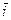 (
(  f/
f/  x)+
x)+ 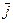 (
(  f/
f/  y)+
y)+ 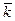 (
(  f/
f/  z),
z),
який називається градiєнтом скалярної функцiї f(x, y, z). Через те, що реакцiя 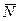 розглядуваної поверхнi нормальна до поверхнi f(x, y, z)= 0, то вона колiнеарна з градiєнтом функцiї f(x, y, z), тобто
розглядуваної поверхнi нормальна до поверхнi f(x, y, z)= 0, то вона колiнеарна з градiєнтом функцiї f(x, y, z), тобто
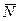 = λ
= λ 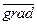 f, (7.7)
f, (7.7)
де λ - множник пропорцiональностi, який в загальному випадку залежить вiд х, у, z. У зв’язку з цим рiвняння (7.6) можна переписати так:
m 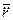 =
= 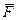 +λ
+λ 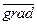 f. (7.8)
f. (7.8)
Спроектуємо обидвi частини цього векторного рiвняння на нерухомi осi декартових координат i одержимо диференцiальнi рiвняння руху матерiальної точки по iдеально гладенькiй поверхнi в такому виглядi:
m 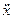 = Fx+λ(
= Fx+λ(  f/
f/  x);
x);
m 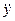 = Fу+λ(
= Fу+λ(  f/
f/  у); (7.9)
у); (7.9)
m 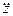 = Fz+ λ(
= Fz+ λ(  f/
f/  z).
z).
Рiвняння (7.9) називаються диференцiальними рiвняннями криволiнiйного руху невiльної матерiальної точки в проекцiях на осi декартової системи координат або рiвняннями Лагранжа першого роду. Цi рiвняння i рiвняння в’язi (7.5) являють собою систему чотирьох рiвнянь, з яких можна визначити чотири невiдомих функцiї х, у, z, λ. В результатi знайдемо закон руху матерiальної точки, а по формулi
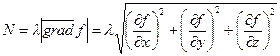
визначаємо модуль нормальної сили реакцiї 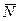 .
.
Якщо на матерiальну точку накладена стацiонарна утримуюча голономна i реальна в’язь, рiвняння якої записано у виглядi (7.5), то рiвняння (7.7) записуються так:
m 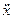 = Fx+ λ(
= Fx+ λ(  f/
f/  x)+Fx тер;
x)+Fx тер;
m 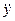 = Fу+λ(
= Fу+λ(  f/
f/  у)+Fy тер; (7.10)
у)+Fy тер; (7.10)
m 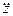 = Fz+ λ(
= Fz+ λ(  f/
f/  z)+Fz тер.
z)+Fz тер.
Проекцiї сили тертя 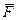 тер можна представити в такому виглядi
тер можна представити в такому виглядi
Fx тер = Fтерcos( 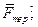
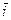 ) = =- Fтерcos(
) = =- Fтерcos( 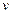
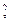
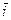 ) =
) =
=- 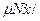 │v│;
│v│;
Fy тер = - μN 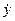 /│v│;
/│v│;
Fz тер = - μN 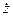 /│v│. (7.11)
/│v│. (7.11)
I тодi рiвняння (7.10) запишуться у виглядi
m 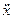 = Fx+ λ(
= Fx+ λ(  f/
f/  x) – μN(
x) – μN( 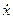 /│v│);
/│v│);
m 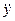 = Fу+λ(
= Fу+λ(  f/
f/  у) – μN(
у) – μN( 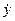 /│v│); (7.12)
/│v│); (7.12)
m 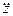 = Fz+ λ(
= Fz+ λ(  f/
f/  z) – μN(
z) – μN( 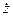 /│v│).
/│v│).
Рiвняння Fтер = μN, (7.5) і (7.12) дають систему рiвнянь, з яких визначають невiдомi х, у, z, N i Fтер.
Дата добавления: 2016-07-18; просмотров: 1992;











