Метод малого параметра

Нелiнiйна механiчна система називається автономною, якщо її рух описується диференцiальним рiвнянням, яке явно не залежить вiд часу. Наприклад:

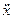+k²x = μf(x, 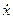), (6.22)

де μ - деякий параметр, f(x, 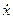) - неперервна нелiнiйна диференцiйована функцiя.

Знайдемо перiодичний розв’язок рiвняння (6.22) в припущеннi, що параметр μ є малою величиною, а функцiя f(x, 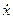) залежить тiльки вiд х. Використаємо метод розкладання в ряд по степенях малого параметра μ i запишемо шуканий розв’язок у виглядi:

x = x₀+μx₁+μx₂+…, (6.23)

де x₀, x₁, x₂ - невiдомi перiодичнi функцiї колової частоти р i частот, кратних р, якi треба знайти. Розкладемо квадрат колової частоти р² по степенях малого параметра μ:

p² = k²+α₁μ+ α₂μ²+…, (6.24)

де α₁ i α₂ - постiйнi коефiцiєнти.

При розв’язуваннi задач методом малого параметра потрiбно дотримуватись такої послiдовностi:

1) скласти диференцiальне рiвняння руху у виглядi

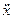+k²x- μf(x) = 0; (6.25)

2) за допомогою формул (6.23) i (6.25) записати шуканий закон руху х i квадрат невiдомої колової частоти р в розкладаннi по степенях малого параметра μ;

3) за допомогою формули (6.23) знайти 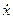i ;

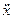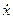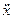4) пiдставити значення х, i та

k² = p² - α₁μ- α₂μ² -...

в формулу (6.25). В результатi пiдстановок одержимо диференцiальне рiвняння з членами, якi утримують рiзнi степенi малого параметра μ, а також з членами без μ;

5) зiбрати в диференцiальному рiвняннi, одержаному в пунктi 4, члени, утримуючi степенi малого параметра μ:

А₀+μА₁+μ²А₂+... = 0;

6) прирiвняти до нуля коефiцiєнти, якi стоять при рiзних степенях малого параметра μ. В результатi одержимо систему диференцiальних рiвнянь

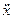₀+р²х₀ = 0;

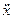₁+р²х₁ = F₁(α₁, х₀); (6.26)

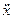₂+p²x₂ = F₂(α₁, α₂, х₀, х₁) i т. д.;

7) записати початковi умови руху для диференцiальних рiвнянь, одержаних в пунктi 6. Наприклад, якщо за умовою при t₀= 0 ми маємо х(0) = а, 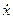(0) = 0, то на основi формул для 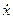i 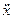пункту 3 одержимо при t₀ = 0

х₀(0) = а, х₁(0) = 0, х₂(0)= 0,...

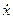₀(0)= 0, 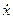₁(0) = 0, 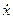₂(0) = 0,...;

8) скориставшись початковими умовами, записаними в пунктi 7, потрiбно проiнтегрувати диференцiальне рiвняння 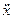₀+р²х₀ = 0 i знайти x₀(t);

9) внести одержаний вираз для x₀(t) в диференцiальне рiвняння

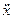₁+р²х₁ = F₁(α₁, х₀),

яке пiсля тригонометричних перетворень записується у виглядi:

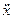₁+р²х₁ = M₁cos(pt)+N₁cos(3t)+… . (6.27)

Для того, щоб x₁ з часом не зростало до нескiнченностi, треба покласти М₁ = 0. З рiвняння М₁ = 0 визначити α₁;

10) скориставшись початковими умовами руху пункта 7, потрiбно проiнтегрувати диференцiальне рiвняння

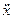₁+р²х₁ = N₁cos(3t)+…

i визначити x₁(t);

11) пiдставити значення x₀(t), α₁ i x₁(t) в диференцiальне рiвняння

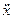₂+p²x₂ = F₂(α₁, α₂, х₀, х₁).

Повторивши викладки пунктiв 9 i 10, визначити α₂ i x₂(t);

12) визначити x(t) i р².

При розв’язуваннi задач ряди слiд обiрвати на членах, якi утримують μ i μ².

Зауваження. Для закріплення матеріалу §6 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 57.3, 57.4;

2) № 57.1, 57.2, 57.5, 57.9;

3) № 57.11, 57.12.

Питання для самоконтролю

1. Чим зумовлена поява в рівняннях руху нелінійних членів?

2. Як розв’язують нелінійні диференціальні рівняння?

3. Як змінюється в першому наближенні модуль сили пружності пружини? До якого диференціального рівняння приводиться задача нелінійних коливань в цьому випадку?

4. Як більш точно записати закон Гука, коли характеристика сили пружності є „жорсткою” та „м’якою”? Якими будуть диференціальні рівняння руху в цих випадках?

5. Як записують диференціальне рівняння нелінійних коливань в загальному випадку?

6. Запишіть нелінійне диференціальне рівняння коливань маятника.

7. Опишіть метод поетапного інтегрування.

8. Яка нелінійна механічна система називається автономною?

9. Опишіть хід розв’язання задач методом малого параметра.

§7. Диференцiальнi рiвняння руху невiльної матерiальної точки