Метод поетапного iнтегрування
Розглянемо цей метод на такому прикладi.
Приклад. На рис. 6.2,a показано тягар А, який може рухатись пiд дiєю двох пружин в прямолiнiйних направляючих. Пружини до тягаря не прикрiпленi. Коефiцiєнти жорсткостi пружин вiдповiдно дорiвнюють с1 i c2. В початковий момент часу тягар знаходився в крайньому правому положеннi i був вiдпущений без початкової швидкостi.
В положеннi рiвноваги пружини не напруженi.
Знайти рiвняння руху тягаря i перiод його вiльних коливань за умови, що сили пружностi пружин описуються законом Гука.
Розв’язання. В положеннi рiвноваги пружини не напруженi i до тягаря не прикрiпленi. При русi тягаря направо вiд нуля до нього прикладена сила пружностi правої пружини, а при русi налiво вiд нуля - лiвої пружини. Характеристика сили пружностi складається з двох прямолiнiйних вiдрiзкiв (рис. 6.2, б).
Перiод коливань складається з чотирьох етапiв:
1) пiд дiєю правої пружини з крайнього правого положення в нульове;
2) пiд дiєю лiвої пружини з нульового положення в крайнє лiве;
3) пiд дiєю лiвої пружини з крайнього лiвого положення в нульове;
4) пiд дiєю правої пружини з нульового в крайнє праве положення.
Розглянемо рух тягаря на першому етапi з крайнього правого положення в нульове. Рух описується диференцiальним рiвнянням
m 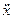 = - c1х,
= - c1х,
тобто
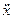 +k12x = 0, (6.6)
+k12x = 0, (6.6)
де
k12 = c1/m.
Загальний розв’язок лiнiйного рiвняння (6.6) має вигляд:
х = C1cos(k1t)+C2sin(k1t). (6.7)
Знаходимо похiдну за часом:
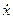 =- C1k1sin(k1t) + C2k1cos(k1t). (6.8)
=- C1k1sin(k1t) + C2k1cos(k1t). (6.8)
Згiдно початкових умов при t0 = 0 x = x0; 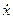 = 0. Пiдставляємо їх в рiвняння (6.7) i (6.8), знаходимо C1 = x0, C2= 0.
= 0. Пiдставляємо їх в рiвняння (6.7) i (6.8), знаходимо C1 = x0, C2= 0.
Значить
x = x0cos(k1t); (6.9)
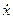 = - x0k1sin(k1t).
= - x0k1sin(k1t).
Рух тягаря на цьому етапi вiдбувається протягом часу
0≤t 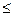 τ1,
τ1,
де τ1  - момент часу, коли тягар приходить в нульове положення. При цьому
- момент часу, коли тягар приходить в нульове положення. При цьому
0 = x0cos(k1 τ1);
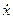 (τ1) = - k1x0sin(k1 τ1). (6.10)
(τ1) = - k1x0sin(k1 τ1). (6.10)
З першого з цих рiвнянь знаходимо
k1 τ1 = π/2,
τ1 = ( π/2 )/k1. (6.11)
Отже початковими умовами для другого етапу є
х = х(τ1) = 0;
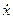 =
= 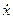 (τ1) = - k1x0. (6.12)
(τ1) = - k1x0. (6.12)
Рух на цьому етапi описується диференцiальним рiвнянням
m 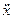 = - c2х,
= - c2х,
тобто
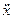 +k22x = 0, (6.13)
+k22x = 0, (6.13)
де позначено k22 = c2/m.
Загальний розв’язок рiвняння (6.13) має вигляд:
x = C3cos(k2t) + C4sin(k2t). (6.14)
Знаходимо похiдну за часом
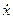 =- C3k2sin(k2t) + C4k2cos(k2t). (6.15)
=- C3k2sin(k2t) + C4k2cos(k2t). (6.15)
Пiдставимо в (6.14) i (6.15) початковi умови (6.12) i знайдемо C3 = 0, C4 = - (k1/k2)x0. В цьому разi рiвняння (6.14) записується так:
x = - (k1/k2)x0sin(k2t). (6.16)
Рiвняння (6.16) описує рух на другому етапi пiд дiєю лiвої частини пружини з нульового положення в крайнє лiве. Цей рух здiйснюється на протязi часу 0≤t 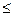 τ2.
τ2.
На другому етапi швидкiсть тягаря дорiвнює
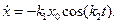
При t = τ2 маємо
х = х(τ2); 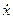 =
= 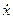 (τ2)= 0
(τ2)= 0
i
x(τ2) = - (k1/k2)x0sin(k2τ2);
0 = - k1x0cos(k2τ2). (6.17)
З другого рiвняння (6.11) знаходимо
k2τ2 = π/2, тобто τ2 =( π/2 )/k2. (6.18)
Пiдставляючи значення τ2 в перше рiвняння (6.17), визначаємо
x(τ2) = - ( k1/k2)x0. (6.19)
Можна сказати, що в момент τ2 тягар знаходиться в крайньому лiвому положеннi i його координата та швидкiсть дорiвнюють
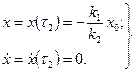 (6.20)
(6.20)
Формули (6.20) є початковими умовами руху тягаря на третьому етапi пiд дiєю лiвої пружини з крайнього лiвого положення в нульове.
На наступних етапах тягар повторить дослiдженi уже рухи: третьому етапу руху тягаря вiдповiдає рiвняння руху, яке описується рiвнiстю (6.13), а четвертому етапу – рівняння руху, яке описується рiвнiстю (6.6). Шуканий перiод Т вiльних коливань тягаря дорiвнює 2(τ1+τ2):
T = π(k1+k2)/ k1k2, (6.21)
де
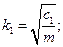
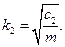
Дата добавления: 2016-07-18; просмотров: 1501;











