Ортогональное проецирование плоскости

Плоскость в пространстве и на чертеже может быть задана следующими способами:

1. Тремя точками, не лежащими на одной прямой - a (АВС);b (DEF).

2. Прямой и точкой, не лежащей на этой прямой - a (АВ, С);b (m, E).

3. Двумя параллельными прямыми - a (АВ || СD);b ( m || n).

4. Двумя пересекающимися прямыми a (АВ Ç СD);b ( m Ç n).

5. Плоской кривой - a (č);b (ň).

Здесь показаны варианты обозначения плоскостей a и b, заданных указанными способами.

5.1. Расположение плоскости относительно плоскостей проекций

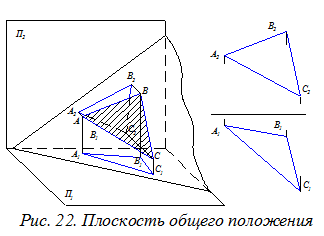
Плоскость общего положения - это плоскость (рис. 22) неперпендикулярная ни одной из плоскостей проекций (П₁, П₂ или П₃). Форма и размеры геометрической фигуры (например, треугольника АВС), задающей такую плоскость на чертеже искажаются.

Плоскости проецирующие – перпендикулярные к одной из плоскостей проекций (рис. 23-25). На указанную плоскость проекций плоскость отображается вырожденно – в виде прямой.

Определение. Вырожденной проекцией плоскости называется прямая ортогонального чертежа, где отобразились все точки этой плоскости (собирательное свойство вырожденной проекции плоскости).

Положение на ортогональном чертеже вырожденной проекции обозначается утолщёнными штрихами с надписью, например, a₁ или b₂. Углы наклона вырожденной проекции плоскости к координатным осям определяет наклон плоскости к соответствующей плоскости проекций (см. на рис. 23, 24 углы j, y, q).

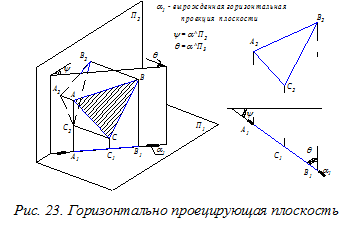Различают горизонтально проецирующие, фронтально проецирующие и профильно проецирующие плоскости (рис. 23-25).

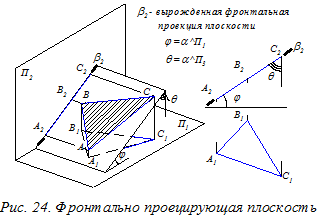Проецирующая плоскость, проходящая через координатную ось, называется осевой. Если осевая плоскость делит пополам прямой двугранный угол, образованный плоскостями проекций, то такая плоскость называется биссекторной (см. рис. 25).

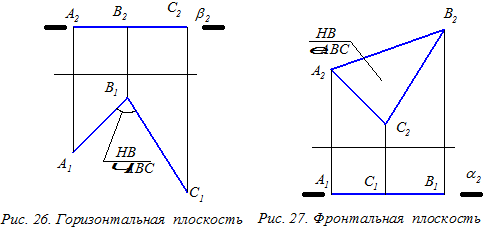
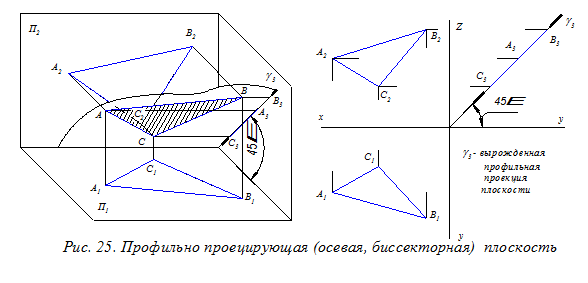Плоскости уровня – это плоскости, параллельные одной из плоскостей проекций (рис. 26 и 27). На эту плоскость проекций любая геометрическая фигура, задающая плоскость отображается неискажённо (в натуральную величину). По отношению к двум другим плоскостям проекций плоскости уровня перпендикулярны (т. е. это дважды проецирующие плоскости). Различают горизонтальную, фронтальную и профильную плоскости уровня.

5.2. Прямая и точка, расположенные в плоскости

Определение 1. Точка расположена в плоскости, если она лежит на какой-либо прямой этой плоскости.

Определение 2. Прямая расположена в плоскости, если она проходит:

а) через две точки, лежащие в этой плоскости;

б) через точку, лежащую в этой плоскости, параллельно линии, принадлежащей этой же плоскости.

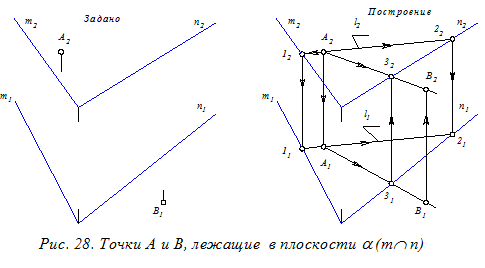На основании этих определений строятся недостающие проекции точки и линии, лежащих в плоскости. Например, требуется построить (рис. 28) проекции отрезка АВ Ì a ( m Ç n), если точки заданы лишь одной своей проекцией, например, А(А₂),В(В₁).Другими словами нужно построить недостающие проекции (А₁ и В₂) точек А и В.

Алгоритм построения:

1. l(l₂) ' A(A₂);

l₂ проводим произвольно.

2. l₁ = 1₁- 2₁;

3. А₁ Î l_1;

4. Строим А₁ В₁, а затем

3 (3₁) = А₁ В₁ Ç n₁;

5. В₂ Î А₂ 3₂;

6. А₂ В₂;

Пример. Построить А₂В₂С₂D₂ фигуры ABCD (А₁В₁С₁D₁) Ì a ( h Ç f).

Построение: 1. Отрезок СB (С₁В₁) продолжим в обе стороны до пересечение его с линиями f и h в точках 1 и 2 соответственно. Далее по линиям связи строим С₂B₂ Ì 1₂2₂.

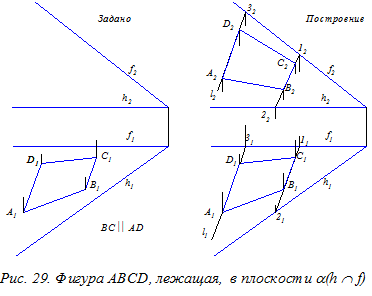2. Аналогично строим A₂D₂ çç В₂D₂.