Аффинная система координат на плоскости
О п р е д е л е н и е. Аффинной системой координат на плоскости (аффинным репером) называется точка и два неколлинеарных вектора: 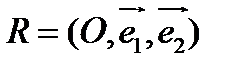 .
.
Прямые 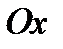 и
и 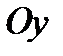 , определяемые точкой
, определяемые точкой  и векторами
и векторами 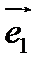 и
и 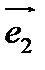 , называются соответственно осью абсцисс и осью ординат.
, называются соответственно осью абсцисс и осью ординат.
Частным случаем аффинной системы координат является прямоугольная система координат 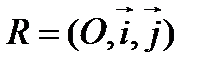 , определяемая точкой
, определяемая точкой  и ортогональными ортами
и ортогональными ортами 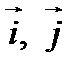 .
.
О п р е д е л е н и е. Вектор 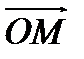 называется радиус-вектором точки
называется радиус-вектором точки 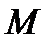 .
.
О п р е д е л е н и е. Координатами точки называются координаты её радиус-вектора: 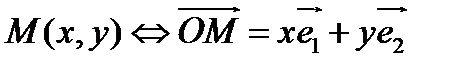 .
.
У п р а ж н е н и е. Построить точку по координатам в заданном аффинном репере.
У п р а ж н е н и е. Найти координаты вершин правильного шестиугольника 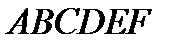 с центром
с центром  относительно аффинной системы координат
относительно аффинной системы координат 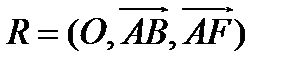 .
.
Отметим простейшие задачи, решаемые с помощью координат
1. Определение координат вектора по координатам начала и конца относительно аффинной системы координат:
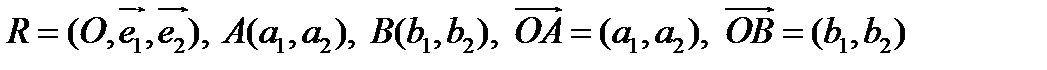 ,
,
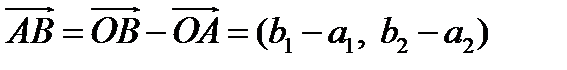 .
.
2. Вычисление координат точки по заданному простому отношению трех точек прямой и координатам двух из них относительно аффинной системы координат.
О п р е д е л е н и е. Простым отношением трех точек  прямой, заданных в указанном порядке, называется число
прямой, заданных в указанном порядке, называется число  , такое, что
, такое, что 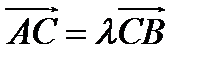 (обозначение
(обозначение 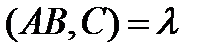 ).
).
У п р а ж н е н и е. На прямой выбраны точки 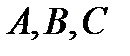 так, что
так, что 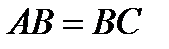 . Определить
. Определить 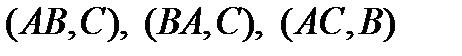 .
.
Имеем 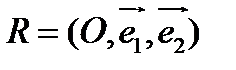 ,
, 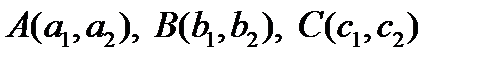 и
и 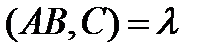 , то есть
, то есть 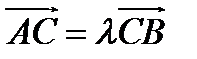 . Переходя к координатам векторов, получим
. Переходя к координатам векторов, получим 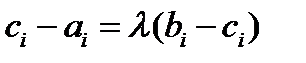
 Отсюда получаем возможность выразить координаты точки
Отсюда получаем возможность выразить координаты точки  :
: 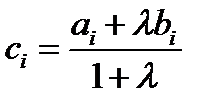 .
.
В частности, если 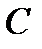 середина
середина 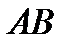 , то
, то 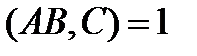 и получаем
и получаем 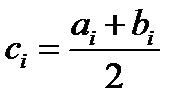 – координаты середины отрезка равны полусуммам соответствующих координат концов отрезка.
– координаты середины отрезка равны полусуммам соответствующих координат концов отрезка.
3. Вычисление расстояния между точками по координатам относительно прямоугольной системы координат.
Имеем 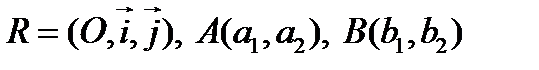 . Расстояние
. Расстояние 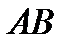 можно найти как длину вектора
можно найти как длину вектора 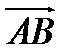 . Поскольку базис ортонормированный, то получаем:
. Поскольку базис ортонормированный, то получаем:
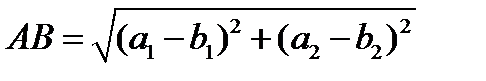
– расстояние между точками равно корню квадратному из суммы квадратов разностей соответствующих координат точек.
Дата добавления: 2021-09-25; просмотров: 735;











