Способ замены плоскостей проекций

Этот способ преобразования эпюра основан на следующем принципе. Геометрическая фигура (прямая или плоскость), занимающая общее положение в исходной системе плоскостей проекций х₁₂ (П₁/П₂), оставаясь неподвижной, проецируется на новую плоскость проекций П₄. При этом новая плоскость проекций должна быть перпендикулярна одной из исходных плоскостей проекций: П₄ ^ П₁ или П₄ ^ П₂. Выбор расположения новой плоскости проекций по отношению к геометрической фигуре связан с необходимостью получения частного положения (параллельного или перпендикулярного новой плоскости проекций) этой фигуры.

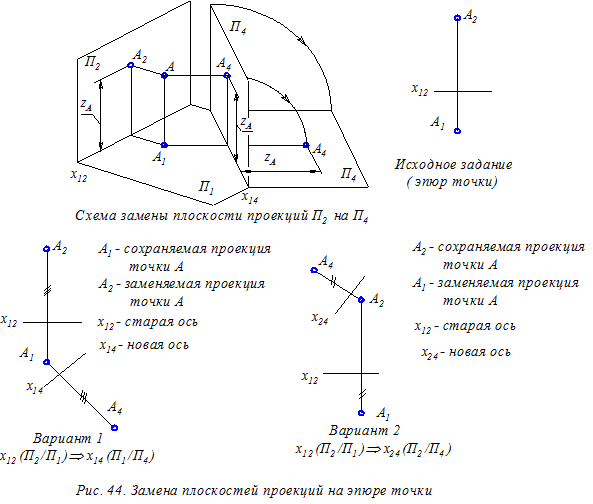
На рис. 44 показана схема замены фронтальной плоскости проекций при проецировании точки А, а также два эпюрных варианта замены плоскостей проекций по отношению к точке А:

Вариант 1. Сохранение в новой системе горизонтальной плоскости проекций П₁ и замена фронтальной плоскости проекций П₂ на П₄.

Вариант 2. Сохранение в новой системе фронтальной плоскости проекций П₁ и замена горизонтальной плоскости проекций П₁ на П₄.

Заметим, что в индексации обозначения оси новой системы плоскостей проекций (новой оси) первым указывают индекс сохраняемой плоскости проекций (например, х₁₄ или х₂₄).

Правило. Для построения проекции точки в новой системе плоскостей проекций необходимо выполнить следующие действия:

1. Из сохраняемой проекции точки перпендикулярно к новой оси провести линию связи.
2. Измерить расстояние от старой оси до заменяемой проекции точки (координату z – при замене по первому варианту; или координату y – при замене по второму варианту).
3. Отложить измеренное расстояние от новой ось, вдоль построенной линии связи.

При преобразовании чертежа решают следующие четыре основные задачи.

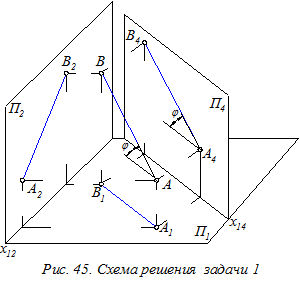Задача 1. Преобразовать чертёж так, чтобы в новой системе плоскостей проекций прямая АВ общего положения стала параллельна одной из плоскостей проекций.

Для решения поставленной задачи новую плоскость проекций П₄ располагают (рис. 45):

а) параллельно заданной прямой;
б) перпендикулярно одной из исходных плоскостей проекций (П₁ или П₂).

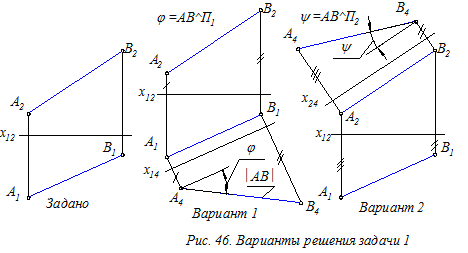Выполнение этих условий на эпюре означает расположение новой оси (х₁₄ или х₂₄) параллельно горизонтальной А₁В₁ (рис. 46, вариант 1) или фронтальной А₂В₂ (рис. 46, вариант 2) проекции прямой АВ. В результате преобразования (на плоскости П₄) кроме НВ отрезка прямой определяются и углы j или y наклона прямой к соответствующей плоскости проекций (П₁ или П₂).

Задача 2. Преобразовать чертёж так, чтобы в новой системе плоскостей проекций прямая АВ общего положения стала перпендикулярна одной из плоскостей проекций.

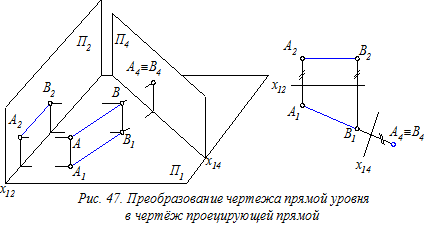Если исходная прямая АВ чертежа является линией уровня (рис. 47), то поставленная задача решается одним преобразованием, т. к. новую плоскость проекций П₄ можно расположить перпендикулярно, как к прямой АВ, так и одной из исходных плоскостей проекций (например, на рис. 47 П₄ ^ АВ и П₄ ^ П₁).

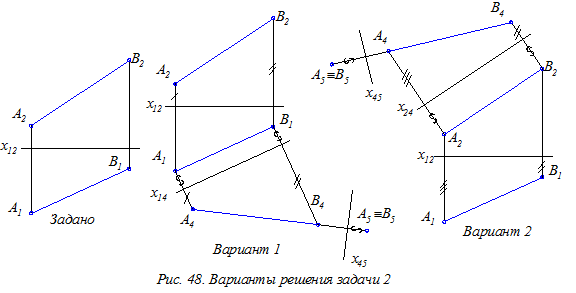Для преобразования чертежа прямой общего положения требуется выполнить две замены (иногда говорят: выполнить полную замену) плоскостей проекций по двум возможным вариантам (рис. 48).

Вариант 1:

а) х₁₂ (П₂/П₁) Þ х₁₄ (П₁ /П₄):

х₁₄ || А₁В₁Þ А₄В₄= çАВ ç – построение прямой, параллельной плоскости проекций П₄;

б) х₁₄ (П₁/П₄) Þ х₄₅ (П₄ /П₅);

х₄₅ ^ çАВ çÞ А₅ º В₅ – построение прямой, перпендикулярной плоскости проекций П₅.

Вариант 2:

а) х₁₂ (П₂/П₁) Þ х₂₄ (П₂ /П₄):

х₂₄ || А₂В₂Þ А₄В₄= çАВ ç – построение прямой, параллельной плоскости проекций П₄;

б) х₂₄ (П₂/П₄) Þ х₄₅ (П₄ /П₅);

х₄₅ ^ çАВ çÞ А₅ º В₅ – построение прямой, перпендикулярной плоскости проекций П₅.

При втором преобразовании следует измерять (а затем откладывать от новой оси х₄₅) расстояние от предыдущей оси (х₁₄ – в варианте 1 или х₂₄ – в варианте 2) до заменяемой проекции точки (А₁ – в варианте 1 или А₂ – в варианте 2). Указанные расстояния помечены на рис. 48 волнистой линией.

Задача 3. Преобразовать чертёж так, чтобы в новой системе плоскостей проекций плоскость общего положения a стала перпендикулярна одной из плоскостей проекций.

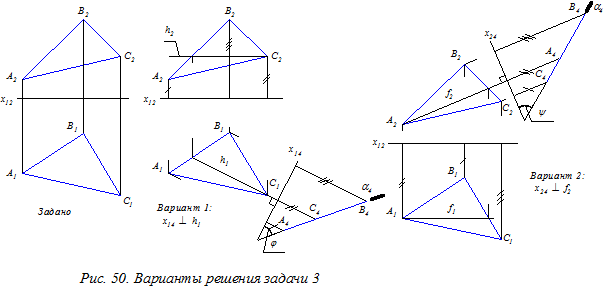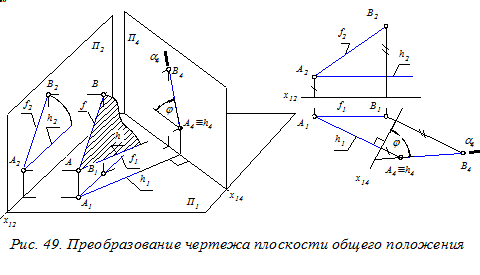
При решении поставленной задачи необходимо новую плоскость проекций П₄ разместить перпендикулярно как заданной плоскости a,так и одной из исходных плоскостей проекций (например, плоскости П₁ на рис. 49). Для выполнения этих условий в заданной плоскости предварительно строят горизонталь h (первый вариант преобразования чертежа) или фронталь f (второй вариант преобразования чертежа) и располагают новую плоскость проекций П₄ перпендикулярно одной из этих линий (рис. 50).

В результате преобразования (на плоскости П₄) кроме вырожденной проекции a₄ плоскости a определяются углы j и y наклона плоскости a к плоскостям проекций П₁ и П₂ соответственно.

Задача 4. Преобразовать чертёж так, чтобы в новой системе плоскостей проекций плоскость a общего положения стала параллельна одной из плоскостей проекций.

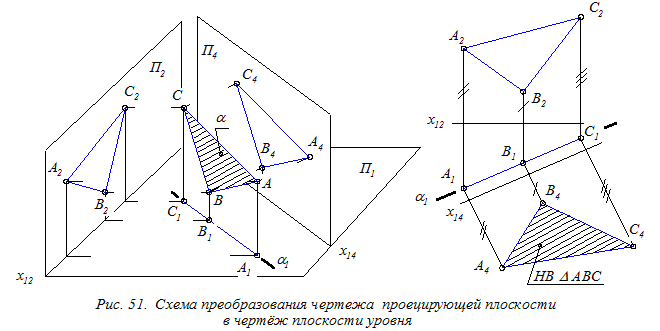
Если бы заданная плоскость была проецирующей, то поставленная задача решалась одним преобразованием, т. к. новую плоскость проекций П₄ можно было разместить параллельно заданной плоскости и одновременно перпендикулярно одной их исходных плоскостей проекций (например, на рис. 51 показано, что П₄ úú a и П₄ ^ П₁). Выполнение указанных условий на эпюре сводится к построению оси новой системы параллельно вырожденной проекции плоскости (см. на рис. 51 х₁₄ çç a₁).

Для чертежа плоскости общего положения решение указанной задачи сводится к двойному преобразованию чертежа по двум возможным вариантам.

Вариант 1: а) х₁₂ (П₂/П₁) Þ х₁₄ (П₁ /П₄),

х₁₄ ^ h₁ Þ a₄ – построение чертежа проецирующей плоскости (a ^ П₄);

б) х₁₄ (П₁/П₄) Þ х₄₅ (П₄ /П₅)

х₄₅ çç a₄ – построение чертежа плоскости уровня (a ççП₅).

Вариант 2: а) х₁₂ (П₂/П₁) Þ х₂₄ (П₂ /П₄),

х₂₄ ^ f₂ Þ a₄ – построение чертежа проецирующей плоскости (a ^ П₄);

б) х₂₄ (П₂/П₄) Þ х₄₅ (П₄ /П₅)

х₄₅ çç a₄ – построение чертежа плоскости уровня (a ççП₅).

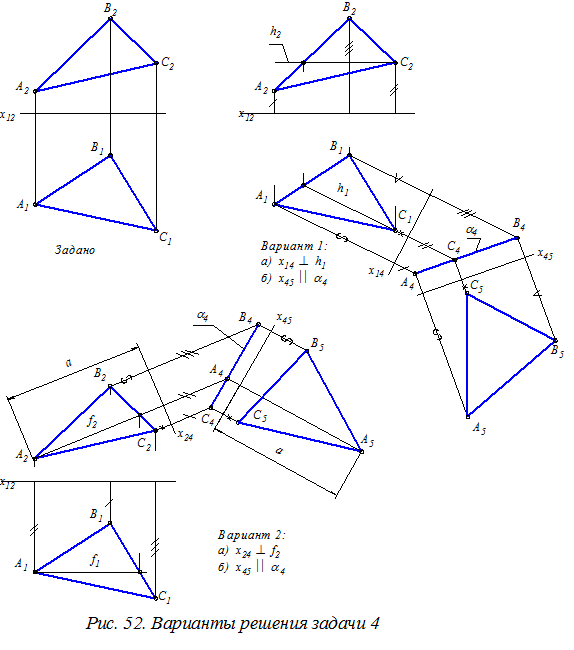В результате преобразования (на плоскости проекций П₅) будет построена натуральная величина плоской фигуры - D АВС. В этом треугольнике можно производить любые построения или измерения (строить высоты, биссектрисы углов, определять величины этих углов и др.).