Примеры преобразований чертежа

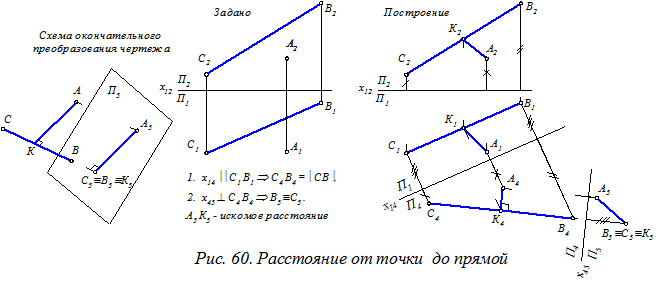Расстояние от точки А до прямой ВС общего положения (рис. 60). Для решения этой задачи следует добиться того, чтобы прямая ВС стала перпендикулярна новой плоскости проекций.

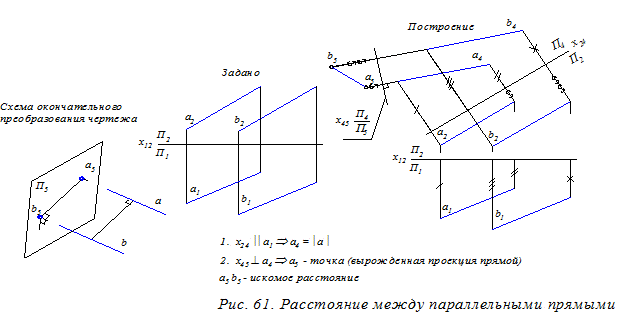Расстояние между параллельными прямыми(aúú b) общего положения (рис. 61). Для решения следует добиться, чтобы обе прямые стали перпендикулярными новой плоскости проекций.

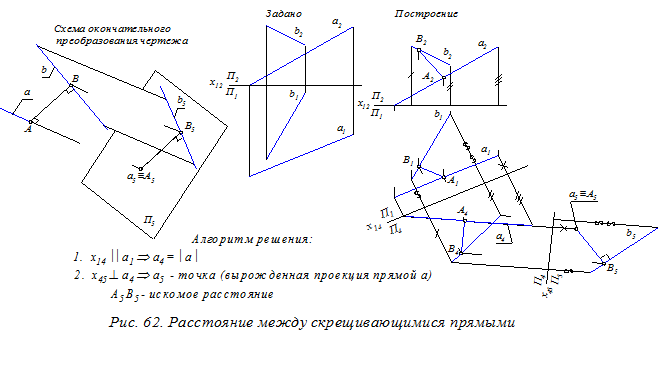Расстояние между скрещивающимися прямыми (рис. 62). Для решения следует добиться, чтобы одна из заданных прямых (например, линия а) стала перпендикулярна новой плоскости проекций. Это достигается двойным преобразованием чертежа (см. ниже алгоритм решения).

Натуральная величина двугранного угла (рис. 63). Двугранным называется угол, образованный двумя пересекающимися плоскостями: a(АВС) Ç b(АВD). Ребром AB такого угла называется линия пересечения этих плоскостей. Мерой величины двугранного угла является плоский угол CKD, образованный в нормальном сечении двугранного угла ( в сечении перпендикулярно его ребру AB). Для решения задачи следует добиться, чтобы ребро АВ двугранного угла расположилось перпендикулярно новой плоскости проекций. Это достигается двойным преобразо
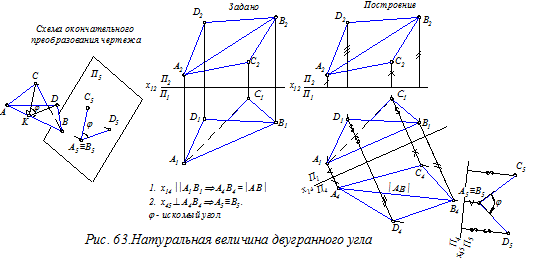ванием чертежа.

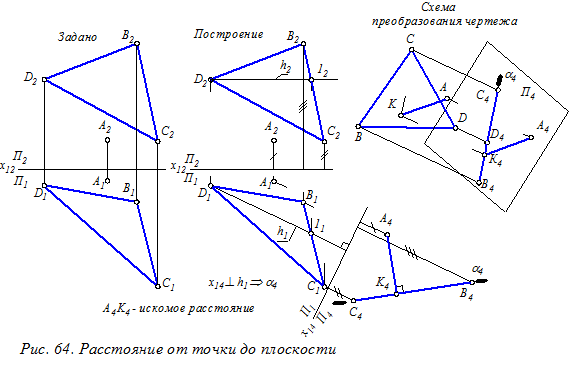
Расстояние от точки А до плоскости a (BCD). Для решения этой задачи следует добиться, чтобы плоскость a стала перпендикулярна новой плоскости проекций П₄ (х₁₄ ^ h₁). Тогда отрезок АК перпендикуляра, проведённого из точки А до пересечения в точке К с плоскостью a, определяющий искомое расстояние, будет располагаться параллельно новой плоскости проекций П₄, т. е отображаться на эту плоскость в натуральную величину.

1. Многогранные поверхности

Многогранником называется геометрическая фигура, ограниченная со всех сторон плоскостями, называемыми гранями.

Совокупность граней многогранника образует многогранную поверхность. Ребром такой поверхности называется прямая – линия пересечения двух смежных граней. Пересечение трех и более смежных граней образует вершину многогранной поверхности.

В курсе НГ рассматриваются следующие позиционные задачи с применением многогранных поверхностей:

- точка, лежащая на многогранной поверхности;

- линия, лежащая на многогранной поверхности;

- сечение многогранной поверхности плоскостью;

- пересечение многогранной поверхности с пространственной линией (частный случай такой задачи – пересечение многогранной поверхности с прямой линией);

- взаимное пересечение двух многогранных поверхностей;

- пересечение многогранной поверхности с кривой поверхностью.

Точка, лежащая на многогранной поверхности. Задача сводится к построению недостающей проекции точки, лежащей на многогранной поверхности. При этом возможны два варианта: точка лежит на ребре такой поверхности или точка лежит на её грани. Оба варианта рассмотрены ранее, как точка, принадлежащая прямой линии и точка, принадлежащая плоскости.

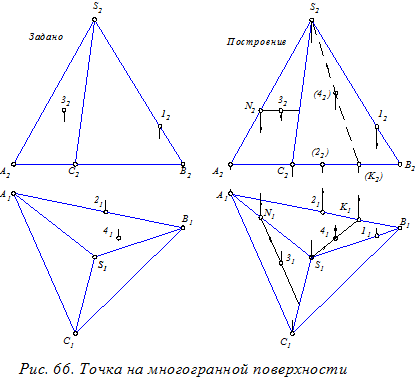
Пример (рис. 66). Построить недостающие проекции точек 1(1₂), 2(2₁), 3(3₂), 4(4₁).

Построение. Недостающие проекции точек 1 и 2, расположенных на рёбрах многогранной поверхности, построены по линиям связи проекций этих точек. Недостающие проекции точек 3 и 4, расположенных на гранях многогранной поверхности построены с применением вспомогательных линий, расположенных на этих гранях и проходящих через заданные точки. Например, линия N3 (N₂3₂) проведена через заданную точку 3(3₂) параллельно ребру АС. Указанную вспомогательную прямую можно назвать горизонталью грани SAC. Линия SK (S₁K₁) проведена через заданную точку 4(4₁) и вершину S(S₁).

Сечение многогранной поверхности плоскостью. В сечении многогранника плоскостью образуется выпуклый многоугольник, число вершин которого равно числу пересекаемых рёбер. Рассмотрим два варианта расположения секущей плоскости: 1) сечение многогранной поверхности проецирующей плоскостью; 2) сечение этой поверхности плоскостью общего положения.

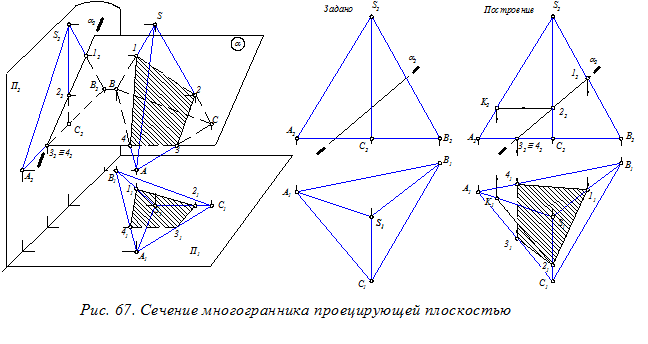
1.Сечение многогранной поверхности проецирующей плоскостью (рис. 67). Фронтальная вырожденная проекция a₂ секущей плоскости a обладает собирательным свойством, по которому определяем фронтальные проекции точек пересечения плоскости a с ребрами многогранника: 1₂ = a₂ Ç S₂В₂; 2₂ = a₂ Ç S₂С₂; 3₂ = a₂ Ç А₂С₂; 4₂ = a₂ Ç А₂В₂;

По линиям связи строим горизонтальные проекции этих точек. Для построения горизонтальной проекции 2₁ точки 2 использована вспомогательная прямая 2-К, расположенная на грани SАC и параллельная ребру АС.

2.Сечение многогранной поверхности плоскостью общего положения (рис. 68). Поставленную задачу удобно решать с применением замены плоскости проекций: х₁₂(П₂/П₁)Þх₁₄ (П₁ /П₄): х₁₄ ^ h₁ Þ a₄. Для построения вырожденной проекции a₄. плоскости a используем две точки (М и Р). Вершины АВС пирамиды имеют нулевую координату z, следовательно их проекции на плоскость П₄ расположатся на координатной оси х₁₄.

После преобразования эпюра на плоскости проекций П₄ легко определяем вершины многоугольника сечения и по линиям связи строим их горизонтальные проекции. Для построения фронтальных проекций 1₂ и 2₂ точек 1 и 2 рекомендуется использовать обратную замену 1₄ на 1₂ (по координате z) и 2₄ на 2₂. Координату z указанных точек измеряем на плоскости П₄ и откладываем
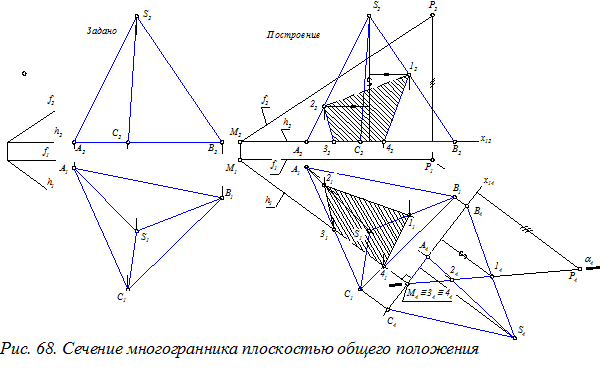на любой вертикальной прямой плоскости П₂.Проводим линии, параллельные координатной оси 0х до пересечения их с соответствующим ребром (см. на рис. 68 линии со стрелками).

В процессе решения задачи необходимо оценивать видимость построенных элементов чертежа.

Пересечение многогранной поверхности S с прямой линией l. Для решения поставленной задачи используется следующий алгоритм (рис. 69):

1. 
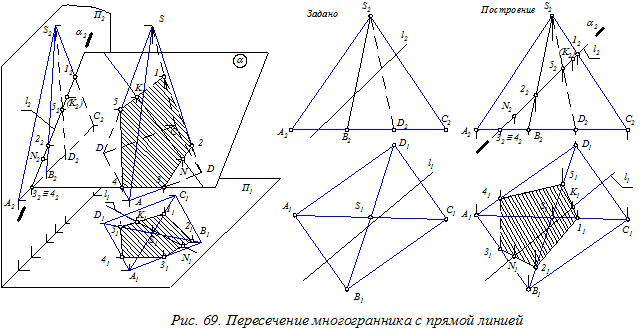
   Через прямую lпроводим вспомогательную плоскость a (обычно проецирующую).
2. Строим фигуру сечения многогранника этой плоскостью: 1-2-3-… =S Ç a.
3. 
   Находим точки пересечения прямой l с фигурой сечения: МК = l Ç 1-2-3-… . Это и будут искомые точки.
4. Оцениваем видимость найденных точек.

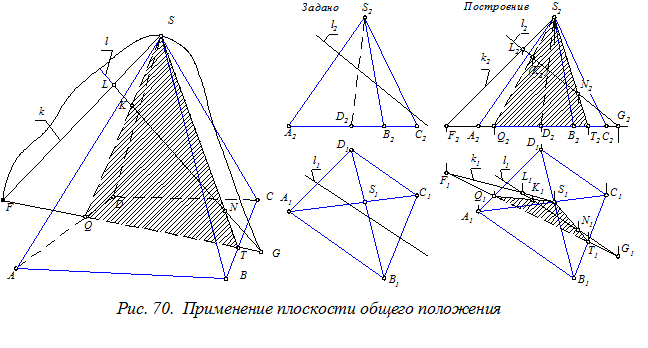
Иногда для решения задачи используют вспомогательную плоскость общего положения, проходящую через заданную прямую и вершину пирамиды (рис. 70)

В этом случае фигура сечения многогранной поверхности плоскостью будет треугольником. Построения производятся в следующей последовательности:

1. Через произвольную точку L, расположенную на прямой l, и вершину S многогранника проводим прямую k.

2. Находим точки G и F пересечения прямых l и k с плоскостью ABCD основания пирамиды.

3.Определяем точки Q и T пересечения прямой FG с линиями основания ABCD и соединяем эти точки с вершиной S.

4. Находим точки K и N пересечения прямой l с D SQT и оцениваем видимость этих точек.

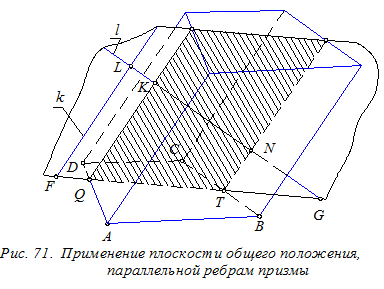
Аналогично может быть решена задача по пересечению призмы с прямой l (рис. 71). Здесь использована вспомогательная плоскость общего положения, проходящая через прямую l параллельно боковым рёбрам призмы. В этом случае рассечение призмы плоскостью произойдёт по параллелограмму.

Кривые поверхности

Основные понятия и определения

Кривая поверхность F может быть образована перемещением в пространстве линии l или поверхности S, которые называются образующими этой поверхности.

В общем случае линия l может быть пространственной кривой произвольной формы, а поверхность S - произвольной кривой поверхностью.

Если линия l является прямой линией, то формируемая с её помощью поверхность называется линейчатой. Если линия l является окружностью, то формируемая с её помощью поверхность называется циклической.

Для задания способа перемещения в пространстве образующей линии (или поверхности) вводятся понятия:

- направляющей линии – это линия, по которой перемещается одна из точек образующей линии (или поверхности);

- плоскость параллелизма – это плоскость, параллельно которой всегда находится образующая линия в своём пространственном перемещении;

- ось вращения – это прямая линия, относительно которой происходит поворот образующей линии (или поверхности).

-линия центров циклической поверхности – это в общем случае пространственная кривая, на которой всегда находится центр образующей окружности в процессе своего пространственного перемещения.

Для построения изображений кривых поверхности на ортогональном чертеже и решения позиционных задач на этих поверхностях используется понятие каркаса поверхности - совокупности линий, расположенных на этой поверхности таким образом, что в общем случае через любую её точку проходит лишь одна линия каркаса.

С точки зрения математики каркас поверхности представляет семейство родственных линий, у которых изменяется лишь один из множества параметров (например, радиус окружности, одна из трёх координат и т.п.), с помощью которых может описываться рассматриваемая поверхность.

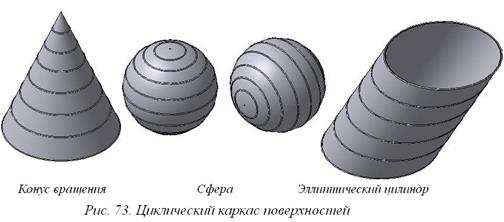
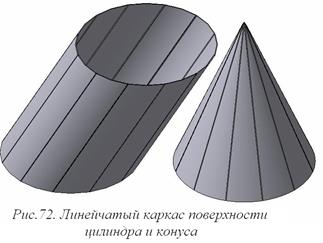
В общем случае на кривой поверхности можно построить множество семейств линий каркаса и среди этого множества интерес представляют простейшие каркасы: линейчатый (рис. 72) или циклический (рис. 73).

Каркас считается непрерывным, если его линии можно провести через любую точку кривой поверхности (сфера, тор, цилиндр, конус, косая плоскость и др.) или дискретным, если на поверхности можно провести ограниченное число линий каркаса (поверхность земли, поверхность крыла и фюзеляжа самолёта, поверхность корпуса судна и др.).

Задание кривой поверхности может быть осуществлено определителем поверхности - совокупностью условий, однозначно определяющих поверхность в пространстве и на чертеже. Рассматривают геометрическую и алгоритмическую части определителя.

Геометрическая часть определителя (ГЧ) – это набор геометрических элементов (точка, прямая, плоскость и т. п.), с помощью которых может быть построен каркас поверхности.

Алгоритмическая часть определителя (АЧ) – формальная последовательность действий с элементами, входящими в ГЧ определителя, позволяющая построить каркас поверхности.

На рис. 74 показаны каркас и определитель цилиндрической и конической поверхностей.