Коллинеарность векторов.

Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

ВОПРОС 23. Смешанное произведение трёх векторов. Компланарность векторов.

Сме́шанное произведе́ние векторов(a, b,c) — скалярное произведение вектора a на векторное произведение векторов b и c:

(a,b,c)=a ⋅(b ×c)

иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами( a,b,c) .

Свойства

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, чтоСмешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и :

Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и , взятому со знаком "минус":

В частности,

Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой.

Компланарность векторов.

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости

Свойства компланарности

Если хотя бы один из трёх векторов — нулевой, то три вектора тоже считаются компланарными.

Тройка векторов, содержащая пару коллинеарных векторов, компланарна.

Смешанное произведение компланарных векторов . Это — критерий компланарности трёх векторов.

Компланарные векторы — линейно зависимы. Это — тоже критерий компланарности.

В 3-мерном пространстве 3 некомпланарных вектора образуют базис.

ВОПРОС 24. Приложения методов аналитической геометрии в исследовании опреаций.

Методами аналитической геометрии исследуются пространственные фигуры. Нужно лишь воспользоваться тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось шкалой, можно задать тремя числами (координатами) положение точки в пространстве

Методы аналитической геометрии исследуют графики алгебраических уравнений, аналитическая геометрия изучает также неалгебраические, или трансцендентные, кривые, например графики экспоненциальных, логарифмических и тригонометрических функций

ВОПРОС 25. Функции вещественного аргумента и числовые последовательности. Основные способы задания.

ВОПРОС 26. Функции вещественного аргумента и числовые последовательности. Основные способы задания.

ВОПРОС 27. . Основные теоремы о пределах.

1. Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa < имеет место неравенство f(x) > M.

lim_{x a}=

1. Функция ограниченная при x a.
2. Функция ограниченная при x .
3. Теорема. Если lim_{x a} f(x)=b, то функция f(x) ограниченная при x a.
4. Бесконечно малые и их свойства. lim_{x a} (x)=0

Теорема. 1. Если f(x)=b+, где  - б.м. при x a, то lim_{x a} f(x)=b и обратно, если lim_{x a}f(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_{x a} (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

1. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_{x a} u(x)=lim_{x a} v(x)=b, то lim_{x a} z(x)=b. ("Теорема о двух милиционерах").

1. Первый замечательный предел.

1. Второй замечательный предел.

Переменная величина

при n® ¥ имеет предел, заключенный между 2 и 3.

ВОПРОС 28.Бесконечно малые величины, основные теоремы о бесконечно малых.

ВОПРОС 29. Бесконечно большие величины, связь бесконечно малых с бесконечными величинами.

ВОПРОС 30. .Дифференцируемость функции, первый дифференциал и производная первого порядка.. Связь непрерывности и дифференцируемости

Пусть функция задана в некоторой области , и -- внутренняя точка этой области. Пусть -- произвольная точка этой же области . Разность называется приращением аргумента ; , где . Разность значений функции называется приращением, или полным приращением функции в точке , соответствующим приращению аргумента ; -- это функция от точки и приращения .

Предположим, что приращение функции можно представить в виде

(7.2

где -- некоторые числа. Подчеркнём, что эти числа не зависят от , но могут измениться, если сменить точку . Относительно величины мы предположим, что это функция, при базе являющаяся величиной большего порядка малости, чем . Это означает, если вспомнить определение бесконечно малой величины большего порядка малости относительно другой бесконечно малой, что

Заметим, что сумма всех слагаемых левой части (7.2), кроме последнего, -- это линейная функция от приращения аргумента , если точка фиксирована. Условие большей малости последнего слагаемого (7.2) относительно означает, что эта линейная функция -- главная часть приращения функции.

Определение 7.11 Если указанное представление (7.2) имеет место, то функцию называют дифференцируемой в точке , а линейную относительно функцию

то есть главную линейную часть приращения функции, -- дифференциалом функции в точке .

Если функция является дифференцируемой в любой точке открытой области , то функцию называют дифференцируемой в области .

Таким образом, приращение дифференцируемой функции можно представить в виде суммы дифференциала , то есть линейной части приращения, и остатка , который имеет более высокий порядок малости, чем приращение :

Теорема 7.8 Дифференцируемая в точке функция является непрерывной в этой точке.

Доказательство. Действительно, если , то стремятся к 0 все слагаемые дифференциала: они имеют вид ; множитель не зависит от , то есть постоянен, а , поскольку Величина также стремится к 0, так как имеет даже больший порядок малости, чем . Значит, . Но условие как раз и означает, что при , то есть что функция непрерывна в точке .

ВОПРОС 31. Правила дифференцирования. Таблица производных.

ВОПРОС 32. Логарифмическое дифференцирование, логарифмическая производная. Приложения логарифмического дифференцирования для вычисления эластичностей функций, применяемых в моделировании таможенных процессов.

ВОПРОС 33.Основные теоремы дифференциального исчисления (теоремы Ферма, Ролля).

ТеоремаФерма

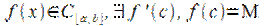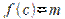Пусть функция или в т.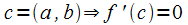

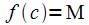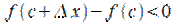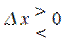Пусть, для определённости, (рис. 10.1), тогда при и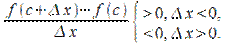

Согласно определению производной имеем

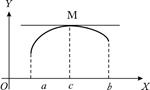
Рис. 10.1

Геометрическоеистолкованиетеоремывытекаетизгеометрическогосмыслапроизводной: касательная к графику функции 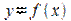в точке с абсциссой 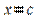параллельна оси .

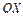Теорема Ролля

Пусть функция 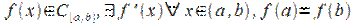. Тогда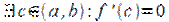

Из условия 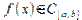следуетпосвойству10непрерывныхна 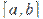функций, что .

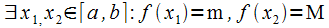Существует две возможности:

1) ;

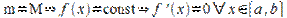2) 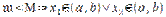в силу .

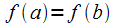Пусть 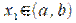, тогда согласно теореме Ферма .

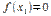Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.

ВОПРОС 34. Теорема Лагранжа (формула конечных приращений). Теорема Коши (обобщённая формула конечных приращений). Связь теоремы Коши с теоремой Лагранжа.

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция 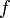непрерывна на отрезке 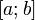и дифференцируема в интервале 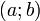, то найдётся такая точка 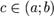, что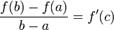

Геометрически это можно переформулировать так: на отрезке 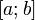найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Теорема Коши́ о среднем значении является обобщением теоремы Лагранжа о конечных приращениях

Пусть на отрезке определены две непрерывные фунции 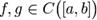. Пусть также 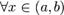существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть 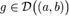, и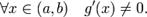

Тогда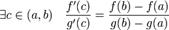

ВОПРОС 35. Функции нескольких переменных. Поверхности и линии уровня, поверхности и кривые безразличия.

Функции нескольких переменных. Определение. Если каждой паре (x,y) значений двух независимых переменных из области W ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y). z=f(x,y)

Геометрическое изображение функции двух переменных - поверхность.

Частное и полное приращение функции.

Полное приращение функции Dz=f(x+Dx, y+Dy)-f(x,y)

Частное приращение функции Dx z=f(x+Dx)-f(x,y)