Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.
Используя эту теорему, запишем разложение определителя третьего порядка по первой строке.
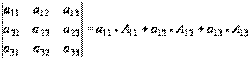
В развернутом виде: 
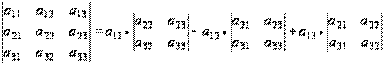 .
.
Последнюю формулу можно использовать как основную при вычислении определителя третьего порядка.
Теорема разложения позволяет свести вычисление определителя третьего порядка к вычислению трех определителей второго порядка.
Рекомендуется раскладывать определитель по той строке или столбцу, где есть нули, т.к. для нулевых элементов не надо находить алгебраические дополнения.
Теорема разложения дает второй способ вычисления определителей третьего порядка.
Теорема разложения позволяет также вычислять определители более высокого порядка, сводя их к вычислению нескольких определителей третьего или второго порядка.
Так, определитель четвертого порядка можно свести к вычислению четырех определителей третьего порядка.
ВОПРОС 10. Обратная матрица. Вычисление обратной матрицы.
Обратную матрицу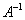 можно найти по следующей формуле:
можно найти по следующей формуле:
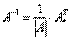 , где
, где 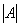 – определитель матрицы
– определитель матрицы 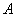 ,
, 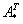 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 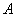 .
.
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как Вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом 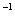
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
Пример:
Найти обратную матрицу для матрицы 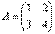
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы. 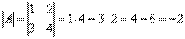
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, 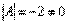 , а значит, всё в порядке.
, а значит, всё в порядке.
2) Находим матрицу миноров 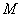
Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.
Матрица миноров имеет такие же размеры, как и матрица 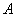 , то есть в данном случае
, то есть в данном случае 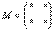 .
.
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице 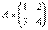
Сначала рассмотрим левый верхний элемент 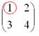
Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:
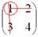
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:
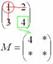
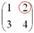
Рассматриваем следующий элемент матрицы 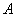 :
: 
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: 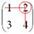
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: 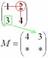
Аналогично рассматриваем элементы второй строки и находим их миноры:

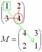
Готово.
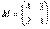 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 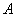 .
.
3) Находим матрицу алгебраических дополнений 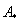
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:
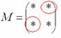
Именно у этих чисел, которые я обвел в кружок!
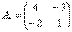 – матрица алгебраических дополнений соответствующих элементов матрицы
– матрица алгебраических дополнений соответствующих элементов матрицы 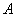 .
.
И всего-то лишь…
4) Находим транспонированную матрицу алгебраических дополнений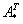 .
.
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.
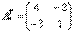 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 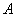 .
.
Ответ.
Вспоминаем нашу формулу 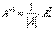
Всё найдено!
Таким образом, обратная матрица:
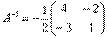
ВОПРОС 11. Системы линейных алгебраических уравнений. Решение систем методом Крамера и матричным методом.
Этот способ или, как его еще называеют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом.
Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A-1, получим A-1AX= A-1B, откуда EX=X=A-1B. Следовательно, матрица-решение X легко находится как произведение A-1 и B.
Для большей ясности решим небольшой пример методом обратной матрицы:
21x1-45x2-3.5x3=10
12x1-16x2+21x3=-16
14x1+13x2-8x3=10
Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что быранг основной матрицы
| A= |
|
и ранг расширенной матрицы
| B= |
|
были равны.
Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.
Для решения методом обратной матрицы необходимо ввести матричные обозначения
| A= |
| X= |
| C= |
| , то X=A-1C |
Найдем обратную матрицу A-1. Как ее найти, показывать не будем. Воспользовавшись нашии онлайн калькулятором, вы сможете выбрать один из двух способов для ее нахождения. Она будет иметь вид.
| A-1= |
|
Для нахождения матрицы X умножим обратную матрицу А-1 на матрицу С
|
| = |
|
Получили решение системы уравнений
X1=0.227
X2=-0.209
X3=-1.194
ВОПРОС 12. . Рант матрицы. Практические приёмы вычисления ранга матрицы.
Определение 4.1.Минором порядка 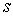 матрицы
матрицы 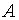 называется определитель квадратной матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких-либо выбранных
называется определитель квадратной матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких-либо выбранных 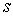 строк и
строк и 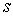 столбцов матрицы
столбцов матрицы 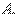
Определение 4.2. В матрице 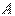 порядка
порядка 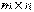 минор порядка
минор порядка 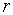 называется базисным, если он не равен нулю, а все миноры порядка
называется базисным, если он не равен нулю, а все миноры порядка 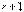 и выше равны нулю, или не существуют вовсе.
и выше равны нулю, или не существуют вовсе.
Определение 4.3. Порядок базисного минора матрицы 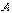 называется рангомматрицы и обозначается символом
называется рангомматрицы и обозначается символом 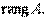
Замечание. Из приведённых определений следует, что ранг матрицы равен наибольшему из порядков её миноров, отличных от нуля.
Одним из способов вычисления ранга матрицы является метод окаймления миноров. Рассмотрим применение этого способа на следующем примере.
Пример. Определить ранг матрицы 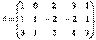
Среди миноров второго порядка матрицы 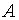 существует, по крайней мере, один, отличный от нуля. Например, минор матрицы
существует, по крайней мере, один, отличный от нуля. Например, минор матрицы 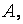 полученный вычёркиванием из этой матрицы третьей строки, третьего, четвёртого и пятого столбцов, отличен от нуля:
полученный вычёркиванием из этой матрицы третьей строки, третьего, четвёртого и пятого столбцов, отличен от нуля: 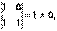
следовательно, ранг данной матрицы не меньше двух.
Найдём миноры третьего порядка матрицы 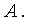 Все десять миноров третьего порядка равны нулю, поэтому ранг данной матрицы не может быть равен трём. Таким образом,
Все десять миноров третьего порядка равны нулю, поэтому ранг данной матрицы не может быть равен трём. Таким образом, 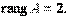
Другой способ вычисления ранга матрицы основан на применении элементарных преобразований матрицы и использовании следующих утверждений.
Теорема 4.1. Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Теорема 4.2. Элементарные преобразования матрицы не изменяют её ранг.
Пример. Вычислим ранг матрицы из предыдущего примера. Для этого матрицу 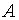 с помощью элементарных преобразований приведём к ступенчатому виду. Найдём сумму второй строки матрицы
с помощью элементарных преобразований приведём к ступенчатому виду. Найдём сумму второй строки матрицы 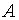 с первой строкой, умноженной на
с первой строкой, умноженной на 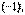 а также сумму третьей строки матрицы
а также сумму третьей строки матрицы 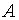 с первой строкой, умноженной на
с первой строкой, умноженной на 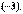 В результате указанных элементарных преобразований получим эквивалентную матрицу
В результате указанных элементарных преобразований получим эквивалентную матрицу 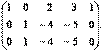
Третью строку полученной матрицы сложим с её первой строкой, умноженной на 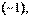 и получимэквивалентную матрицу
и получимэквивалентную матрицу 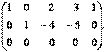
Удалим из этой матрицы третью строку и получим ступенчатую эквивалентную матрицу, количество ненулевых строк которой равно двум: 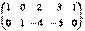
В соответствии с теоремой 4.1, ранг полученной матрицы равен двум, а значит (теорема 4.2), 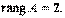
ВОПРОС 13. Теорема Кронекера-Капелли. Решение систем линейных алгебраических уравнений в соответствии с теоремой Кронекера-Капелли.
Необходимость
Пусть система совместна. Тогда существуют числа 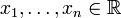 такие, что
такие, что 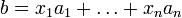 . Следовательно, столбец
. Следовательно, столбец 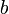 является линейной комбинацией столбцов
является линейной комбинацией столбцов 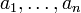 матрицы
матрицы 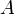 . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 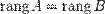 .
.
Достаточность
Пусть 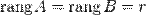 . Возьмем в матрице
. Возьмем в матрице 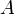 какой-нибудь базисный минор. Так как
какой-нибудь базисный минор. Так как 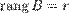 , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы 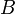 . Тогда согласно теореме о базисном миноре последний столбец матрицы
. Тогда согласно теореме о базисном миноре последний столбец матрицы 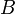 будет линейной комбинацией базисных столбцов, то есть столбцов матрицы
будет линейной комбинацией базисных столбцов, то есть столбцов матрицы 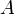 . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы
. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы 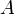
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
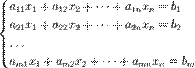
| (1) |
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.
Здесь 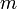 — количество уравнений, а
— количество уравнений, а 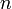 — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
— количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
| c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
ВОПРОС 14. Приложения методов линейной алгебры в моделировании таможенных процессов
Анализ численных методов решения систем линейных алгебраических уравнений, вычисления определителей и обратных матриц; реализация этих методов в виде машинных программ на языке высокого уровня и практическое решение задач на ЭВМ.
В общем случае система линейных алгебраических уравнений имеет вид

В матричной форме система (1) представляется как
A X =В где

Чтобы такая система уравнений имела единственное решение, входящие в нее n уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является неравенство нулю определителя данной системы, т.е. det A ¹ 0. Алгоритмы решения систем уравнений такого типа делятся на прямые и итерационные.
ВОПРОС 15. Прямая на плоскости. Взаимосвязь различных видов уравнений прямой.
Рассмотрим различные виды уравнений прямой на плоскости.
Пусть прямая проходит через точку М0 (x0,y0) перпендикулярно вектору n = {A,B}. Тогда вектор , где М(х,у) — произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению
А(х — х0) + В(у — у0) = 0 - (7.3)
уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Замечание. Вектор n называется нормалью к прямой.
Преобразуем уравнение (7.3) к виду:
Ах + Ву + (-Ах0 — Ву0) = 0.
Обозначив -Ах0 — Ву0 = С, получим общее уравнение прямой:
Ах + Ву + С = 0. (7.4)
Получим теперь уравнение прямой, проходящей через точку М0 (x0,y0) параллельно вектору q = {l,m}. Так как вектор , где М(х,у) — произвольная точка прямой, коллинеарен q, координаты любой точки данной прямой удовлетворяют уравнению
, (7.5)
называемому каноническим уравнением прямой. Вектор q при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М1(х1,у1) и М2(х2,у2), ее направляющим вектором можно считать , и из уравнения (7.5) следует:
- (7.6)
параметрические уравнения прямой.
Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k — тангенс угла, образованного прямой и осью Ох, и записать уравнение
у l прямой в виде:
у = kx + b - (7.8)
Дата добавления: 2016-07-18; просмотров: 5359;











