Неполные уравнения плоскости.

Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным.

Рассмотрим возможные виды неполных уравнений:

1) D = 0 — плоскость Ax + By + Cz = 0 проходит через начало координат.

2) А = 0 — n = {0,B,C}Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.

3) В = 0 — плоскость Ax + Cz +D = 0 параллельна оси Оу.

4) С = 0 — плоскость Ax + By + D = 0 параллельна оси Оz.

5) А = В = 0 — плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох иОу).

6) А = С = 0 — плоскость Ву + D = 0 параллельна координатной плоскости Охz.

7) B = C = 0 — плоскость Ax + D = 0 параллельна координатной плоскости Оуz.

8) А = D = 0 — плоскость By + Cz = 0 проходит через ось Ох.

9) B = D = 0 — плоскость Ах + Сz = 0 проходит через ось Оу.

10) C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.

11) A = B = D = 0 — уравнение Сz = 0 задает координатную плоскость Оху.

12) A = C = D = 0 — получаем Ву = 0 — уравнение координатной плоскости Охz.

13) B = C = D = 0 — плоскость Ах = 0 является координатной плоскостью Оуz.

Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду: (8.3) называемому уравнением плоскости в отрезках. Способ преобразования показан в лекции 7. Параметры а, b и сравны величинам отрезков, отсекаемых плоскостью на координатных осях.

ВОПРОС 16. Плоские кривые второго порядка (эллипс, гипербола, парабола). Канонические уравнения кривых второго порядка.

Плоские кривые.
Все множество плоских кривых можно разделить на циркульные и лекальные.
Циркульнойназыв. кривую, кот.можно построить с помощью циркуля. Это окружность, овал, завиток.

Эллипс - кривая второго порядка, сумма расстояний от любой точки которой до двух фиксированных точек, называемых фокусами, есть величина постоянная, равная большой оси эллипса.

Парабола - кривая второго порядка, расстояние от любой точки которой до фокуса равно расстоянию от этой точки до некоторой фиксированной прямой, называемой директрисой.

Гипербола - кривая второго порядка, разность расстояний от любой точки которой до двух фокусов есть величина постоянная, равная действительной оси гиперболы. Вдоль действительной оси расположены ветви гиперболы.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида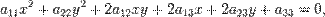

в котором по крайней мере один из коэффициентов 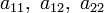отличен от нуля.

Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду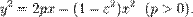

Уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых 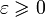от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при 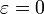кривая является окружностью, при 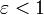— эллипсом, при 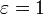— параболой, при 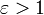— гиперболой.

Уравнение директрисы кривой выражается уравнением 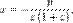а координаты фокуса 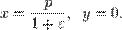Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно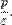

ВОПРОС 17. Плоскость в пространстве. Взаимосвязь различных видов уравнений плоскости.

Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида: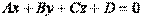

Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку и два произвольных приложенных к этой точке неколлинеарных вектора: 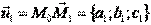и .

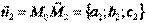-векторноеур-е плоскости.

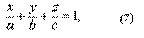
(7)- Уравнение (7) называют уравнением плоскости в отрезках на осях, т.к. числа a, b, c имеют простой геометрический смысл: а - абсцисса точки пересечения плоскости с осью Ох, b - ордината точки пересечения плоскости с осью Оу, с - аппликата точки пересечения плоскости с осью Oz.

ВОПРОС 18. Прямая в пространстве. Основные формы уравнения прямой.

Векторно-параметрическое уравнение прямой :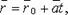

где 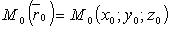- фиксированная точка, лежащая на прямой; 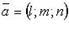-направляющий вектор.

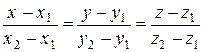- это называют уравнениями прямой, проходящей через две заданные точк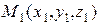и и .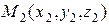

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

=

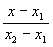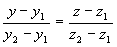
3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a(m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

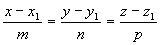
ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ:

Уравнение прямой с угловым коэффициентом:y= kx + b

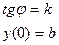
Уравнение прямой в отрезках: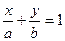

Общее уравнение прямой: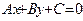

Уравнение с данным направляющим вектором и проходящей через данную точку:

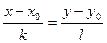
Уравнение прямой с данным вектором нормали

и проходящей через данную точку: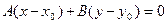

ВОПРОС 19. Сложение векторов, умножение векторов на числа. Вычитание векторов.

Суммой двух векторов и называется вектор , направленный из начала вектора в конец вектора при условии, что начало совпадет с концом вектора . Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Рассмотрим это на примере декартовой системы координат. Пусть

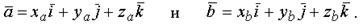
Покажем, что

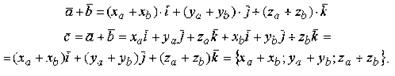
Из рисунка 3 видно, что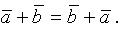

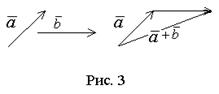
Сумма любого конечного числа векторов может быть найдена по правилу многоугольника (рис. 4): чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

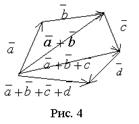
Свойства операции сложения векторов:

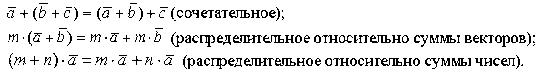
В этих выражениях m, n - числа.

Разностью векторов и называют вектор Второе слагаемое является вектором, противоположным вектору по направлению, но равным ему по длине.

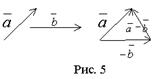
Таким образом, операция вычитания векторов заменяется на операцию сложения

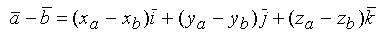
Вектор , начало которого находится в начале координат, а конец - в точке А (x1, y1, z1), называют радиус-вектором точки А и обозначают или просто . Так как его координаты совпадают с координатами точки А, то его разложение по ортам имеет вид

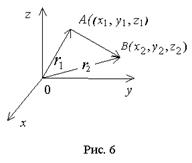
Вектор , имеющий начало в точке А(x1, y1, z1) и конец в точке B(x2, y2, z2), может быть записан в виде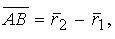

где r₂- радиус-вектор точки В; r₁- радиус-вектор точки А.

Поэтому разложение вектора по ортам имеет вид

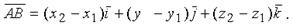
Его длина равна расстоянию между точками А и В

УМНОЖЕНИЕ

Так в случае плоской задачи произведение вектор на a = {ax; ay} на число b находится по формуле

a · b = {ax · b; ay · b}

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение

3 · a = {3 · 1; 3 · 2} = {3; 6}

Так в случае пространственной задачи произведение вектора a = {ax; ay; az} на число b находится по формуле

a · b = {ax · b; ay · b; az · b}

Пример 1. Найти произведение вектора a = {1; 2; -5} на 2.

Решение

2 · a = {2 · 1; 2 · 2; 2 · (-5)} = {2; 4; -10}

ВОПРОС 20. Модуль вектора, направляющие косинусы.

Множество векторов на прямой назовем одномерным векторным пространством 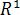, множество векторов на плоскости – двумерным векторным пространством 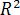, в пространстве – трехмерным векторным пространством 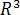. Пространство 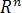является системой содержащей всю бесконечную совокупность -мерных векторов.

В пространстве 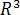обычно используют прямоугольную декартову систему координат где любая точка М пространства, имеющая координаты X (абсциссу), Y (ординату) и Z (аппликату), обозначается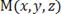

Определение. Вектор , начало которого находится в начале координат, а конец в точке

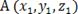, называют радиус–вектором точки A и обозначают 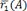или просто 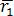. Так как его координаты совпадают с координатами точки A , то его разложение по ортам имеет вид /

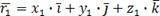Вектор , имеющий начало в т. 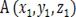, и конец в т. 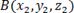, может быть записан в ви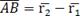де , где 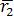– радиус-вектор точки В ; 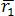– радиус-вектор точкиА.

Поэтому разложение вектора по ортам имеет вид: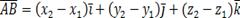

Его длина равна расстоянию между точками А и В: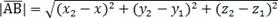

Свободный вектор 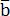, например , заданный в координатном пространстве 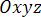, может быть представлен в ви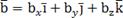де , где 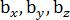– проекции вектора 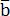на соответствующие оси координат (координаты вектора), а 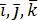– орты этих осей. Пишут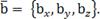

Длина вектора (модуль вектора) определяется по формуле: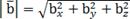

Направление вектора определяется углами 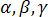, образованными им с осями координат 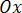, , 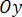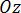. Косинусы этих углов (направляющие косинусы вектора) вычисляются по формулам: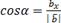

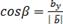
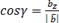
Тогда координаты вектора будут равны:

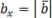
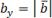
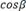
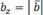
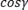
Подставив эти выражения в формулу вычисления длины вектора,

установим, что направляющие косинусы вектора связаны соотношением:

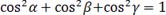
ВОПРОС 21. Скалярное произведение векторов. Угол между двумя векторами. Условие ортогональности двух векторов. Проекция вектора на заданное направление

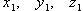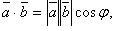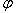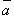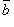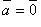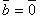Скалярное произведение векторов и где - угол между векторами и ; если либо , то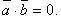

Из определения скалярного произведения следует, что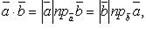

где, например, 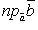есть величина проекции вектора 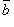на направление вектора .

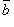Скалярный квадрат вектора: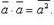

Свойства скалярного произведения:

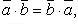
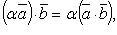
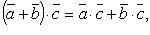
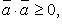
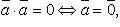
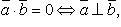
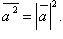
Скалярное произведение в координатах

Если 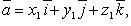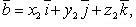то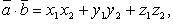

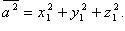
Угол между векторами

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними

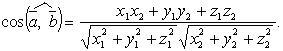
Условие ортогональности двух векторов:

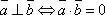или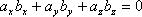

Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.

Проекция вектора на заданное направление

Нахождение проекции вектора а на направление, заданное вектором b, может осуществляться по формуле

ВОПРОС 22. Векторное произведение двух векторов. Коллинеарность векторов. Векторное произведение(Векторное произведение двух векторов. )— это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

Векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.

В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности»