Полупространство. Уравнение п-ва.

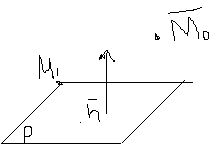
называется нормальным вектором

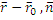( )≥0 для верхнего полупространства

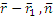( )≤0 для нижнего полупространства

,

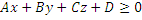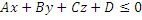
Рассмотрим какую-то т. 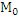и ее координаты подставим. Если знаки одинаковы,то по одну сторону, если знаки разные, то по разные стороны плоскости.

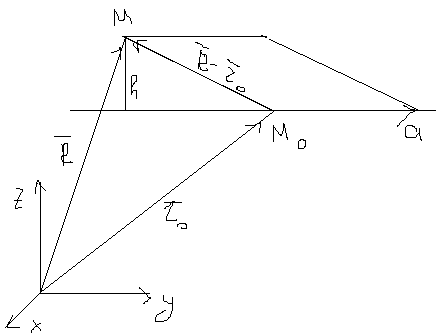
Расстояние от точки до плоскости в векторном виде.

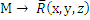
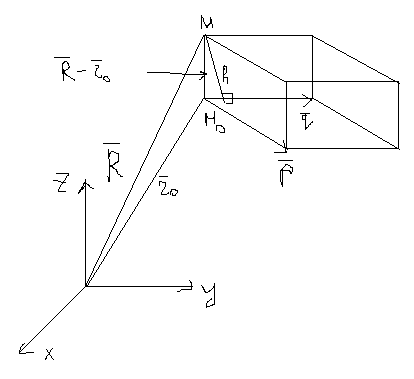Векторы 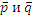определяют плоскость,

h- расстояние до плоскости

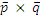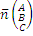[ ]= Нормированный вектор плоскости

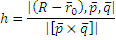
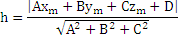
Предложение2. Расстояние от точки до плоскости и скалярном виде.

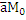Прямая : , М: 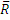(x,y,z,)

Построим параллелограмм по векторам 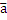и .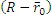

Тогда расстояние от точки до прямой будет высота этого параллелограмма:

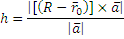
Имеем формулу для расстояния от точки до прямой

Ах+Ву+С=0 ,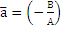

H=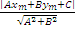

Нормированное уравнение пл-ти.

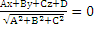
x 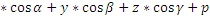= 0 направляющий косинус

Расстояние от точки до прямой в пр-ве и на пл-ти.

Нормированное уравнение прямой на пл-ти.

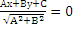
x 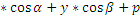= 0 направляющий косинус

Расстояние между непараллельными прямыми в пр-ве.

Вычисление углов между непараллельными прямыми в пр-ве и на пл-ти.

Некоторые задачи на построение.

Перпендикуляр из точки на плоскость и на прямую.