Свойства определителей.. № 9.(Разложение определителей по строке или столбцу).

Определитель n-го порядка, n>1, равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Пример.Вычислим определитель из предыдущего примера разложением по второй строке:

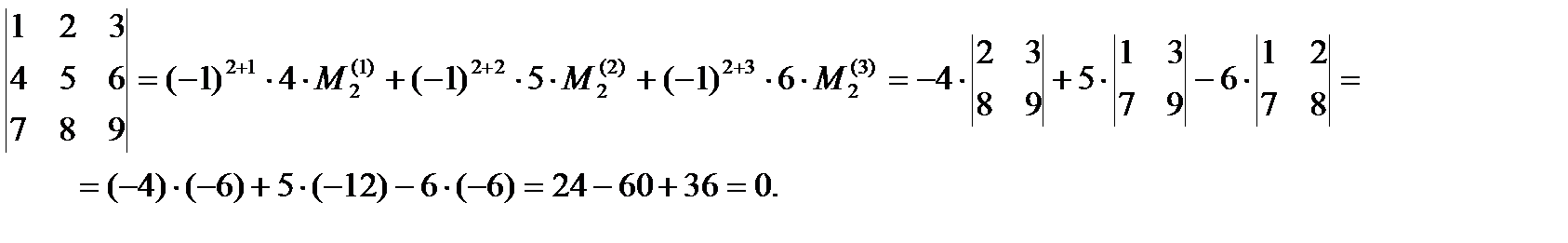Следствие. Определитель треугольной матрицы равен произведению диагональных элементов. (Доказать самостоятельно).

Свойства определителей.. № 10.(Сумма произведений элементов строки, умноженных

На число на Алгебраические дополнения другой строки).

Алгебраические дополнения и миноры

Минором матрицы порядка r называется определитель, составленный из элементов, расположенных на пересечении любых r строк и r столбцов матрицы;

обозначаем M_r.

Пример.

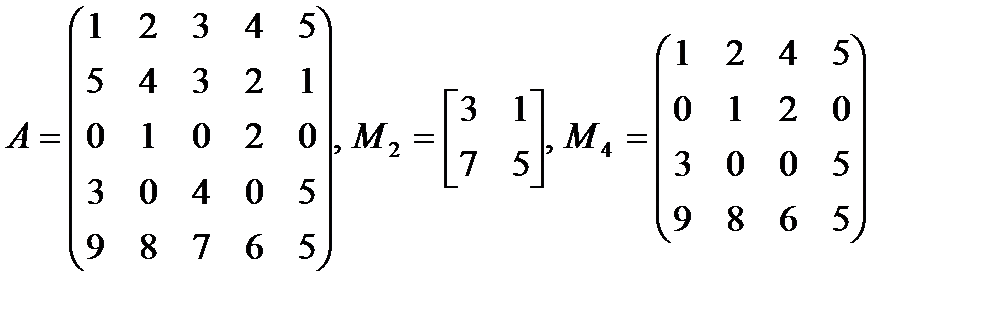
минор M₂ расположен на пересечении 2-й и 5-й строк с 3-м и 5-м столбцами, а минор M₄ — на пересечении 1-й, 3-й, 4-й и 5-й строк с 1-м, 2-м, 4-м и 5-м столбцами.

Минор M_r, расположенный в первых r строках и в первых r столбцах, называется угловым или главным минором.

Решение и исследование системы 3-х уравнений 1-й степени с 3-мя неизвестными – Определитель системы не равен 0.(Правило Крамера). (Получение формулы на основе разложения определителя)

219. Решение и исследование системы 3-х уравнений 1-й степени с 3-мя неизвестными –Δ

системы равен 0, но Δx= Δy= Δz=0.

220. Решение и исследование системы 3-х уравнений 1-й степени с 3-мя неизвестными – Δ

системы равен 0, но Δx= Δy= Δz=0.

Сведение произвольной системы 3-х уравнений 1-й степени с 3-мя неизвестными к однородной системе 3-х уравнений 1-й степени с 3-мя неизвестными

Понятие определителя любого порядка .Перестановки индексов.

Формула полного разложения определителя по элементам матрицы.