Основные свойства умножения матриц и их произведения

Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

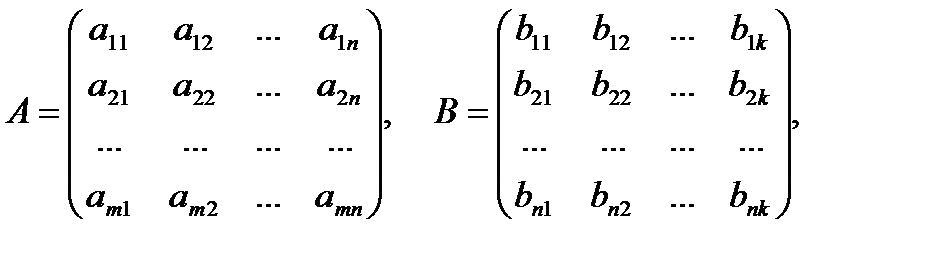
то произведением матриц A и B называется матрица

,

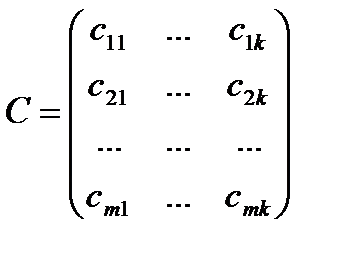элементы которой вычисляются по формуле

, ;

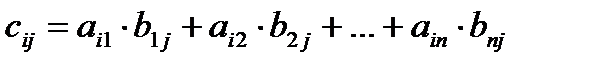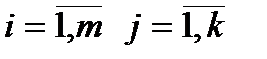произведение матриц A и B обозначается AB: C=AB.

Пример:

.

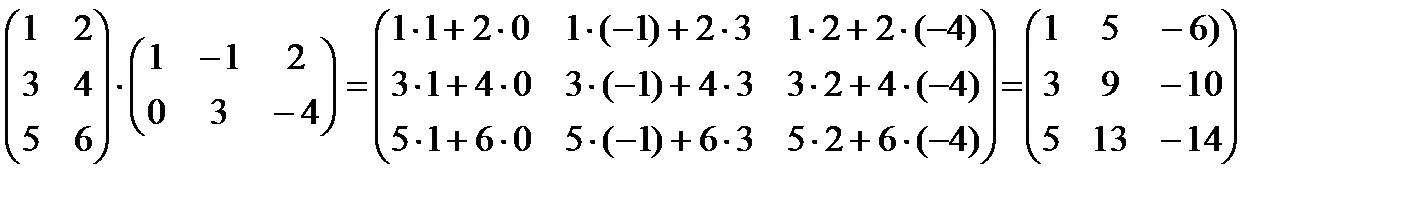Для произведения матриц соответствующих порядков справедливо:

1. A·B ≠ B·A,

2. (A + B) · C = A·C + B·C,

3. C·(A + B) = C·A + C·B,

4. α(A·B) = (αA) ·B,

5. (A·B) ·C = A·(B·C).

Если AB = BA, то матрицы A и B называются перестановочными.

Для квадратных матриц определена единичная матрица — квадратная матрица, все диагональные элементы которой единицы, а остальные — нули:

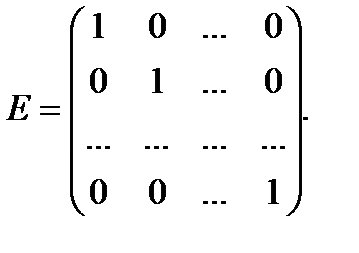
Единичная матрица чаще всего обозначается буквой E или E_n, где n —порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы AE=EA=A.

Основные свойства алгебраических операций над матрицами.

Для операций сложения и умножения матрицы на число справедливо:

1·A=A,

0·A= 

α(βA) = (αβ)A,

A+(B+C) = (A+B)+C,

A+B = B+A,

(α+β)A=αA+βA,

α(A+B) = αA+αB.

где A, B, C — произвольные матрицы одинаковой размерности, — нулевая матрица той же размерности (читается «тэта»), и — произвольные числа.