Уравнение прямой, проходящей через две точки.

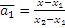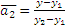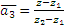
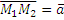, , направляющий вектор прямой.

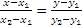на плоскости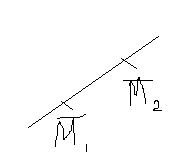

Уравнение плоскости, проходящей через три точки.

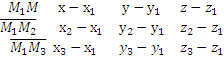= 0

Условие комплонарности трех векторов:

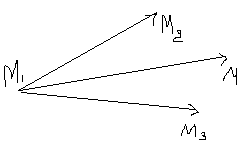
Признаки параллельности прямой и плоскости.

Уравнение прямой:

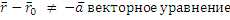
Уравнение плоскости:

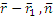( )=0

Направление векторные плоскости:

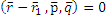
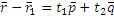
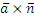( )=0 условие параллельности прямой и плоскости:

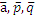( )=0

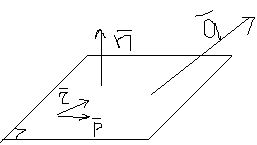
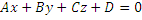
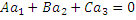
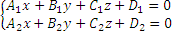
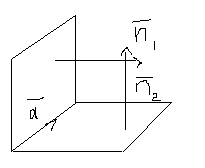Пусть прямая задана пересечением двух плоскостей,

= , ,

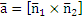
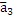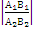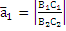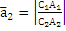
Подставим в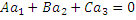

Получаем: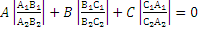

= 0

Определитель третьего порядка, вычислим по правилу звездочки.

Три плоскости пересекаются в одной точки тогда и только тогда, когда определитель составленный из их коэффициентов равено нулю.

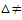при 0

Уравнения в отрезках плоскости и прямой.

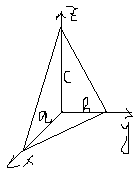Плоскости в пространстве:

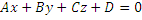
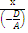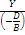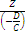+ + -1 = 0

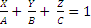
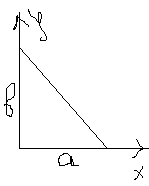Прямой на плоскости:

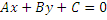
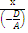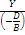+ + -1 = 0

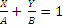
Предложение1 .О коэффициентах уравнений в отрезках.

Если плоскость задана уравнением общего вида, то числа a,в,c в этом уравнении означают длины отрезков отсекаемых этой плоскостью по осям координат.

Аналогично для прямой.