Метод Гаусса решения систем линейных уравнений путем приведения их к треугольному виду.

Метод Гаусса — точный метод решения систем линейных алгебраических уравнений.

Метод Гаусса (его еще называют методом гауссовых исключений) состоит в том, что совместную систему n линейных алгебраических уравнений относительно n неизвестных 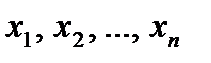(определитель матрицы системы отличен от нуля)

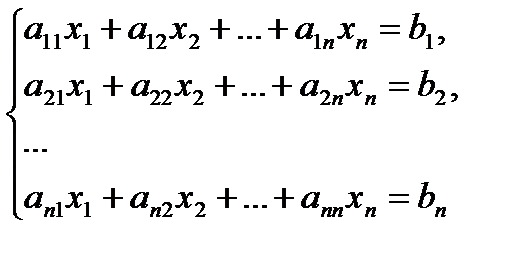
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

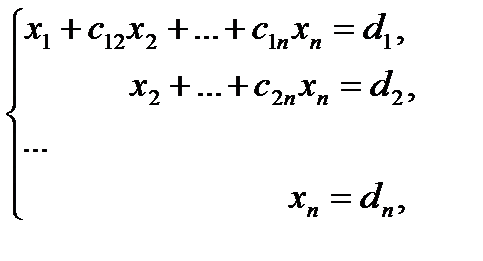
решение которой находят по рекуррентным формулам

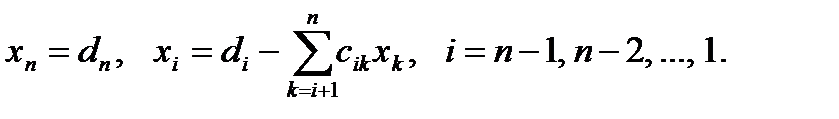
В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными преобразованиями над строками приводят расширенную матрицу системы к ступенчатому виду:

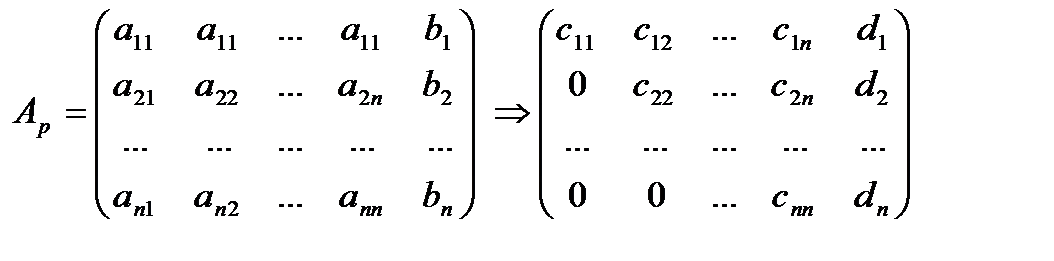
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась диагональная матрица

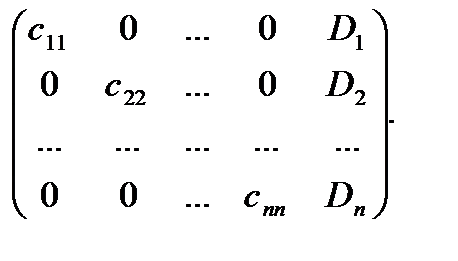
В результате получаем решение системы:

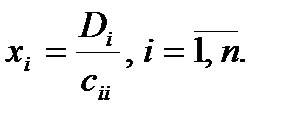
Опишем метод Гаусса последовательно.

Прямой ход

Рассмотрим расширенную матрицу системы

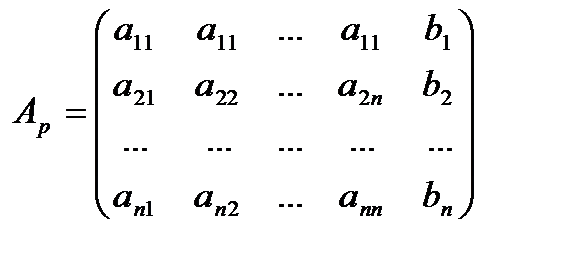
1-й шаг

Предположим, что a₁₁ ≠ 0.

Если это не так, и a₁₁ = 0, переставим строки матрицы так, чтобы a₁₁ ≠ 0. Это всегда возможно, т.к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна.

Элемент a₁₁ ≠ 0 называется ведущим элементом.

Итак, a₁₁ ≠ 0.

Умножим первую строку на число 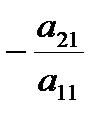и прибавим ко второй строке,

затем умножим первую строку на число 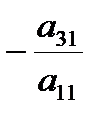и прибавим к третьей строке, и т.д.,

т.е. последовательно умножаем первую строку на число 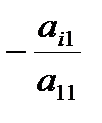и прибавляем к i-й строке, для i=2, 3, …, n.

Получим на первом шаге:

.

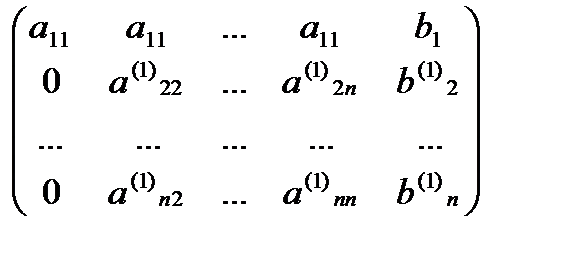2-й шаг

Предположим, что a⁽¹⁾₂₂ ≠ 0.

Если это не так, и a⁽¹⁾₂₂ = 0, переставим строки матрицы так, чтобы a⁽¹⁾₂₂ ≠ 0.

Здесь ведущий элемент a₂₂ ≠ 0.

Умножим вторую строку на число 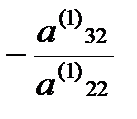и прибавим к третьей строке,

затем умножим вторую строку на число 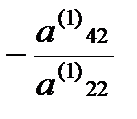и прибавим к четвертой строке, и т.д.,

т.е. последовательно умножаем вторую строку на число 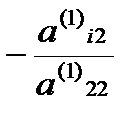и прибавляем к i-й строке, для i=3, 4, …, n.

Получим на втором шаге:

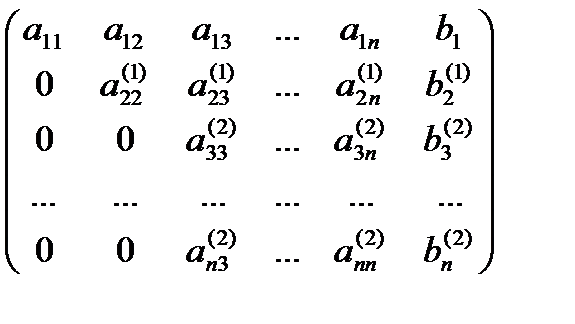
k-й шаг

Предположим, что a^(k-1)_kk≠ 0.

Если это не так, и a^(k-1)_kk = 0, переставим строки матрицы так, чтобы a^(k-1)_kk ≠ 0.

Ведущий элемент a^(k-1)_kk≠ 0.

Умножим k-ю строку на число 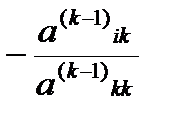и прибавим к i-й строке, для i=k+1, k+2, …, n.

Выполнив n-1 шаг получим:

.

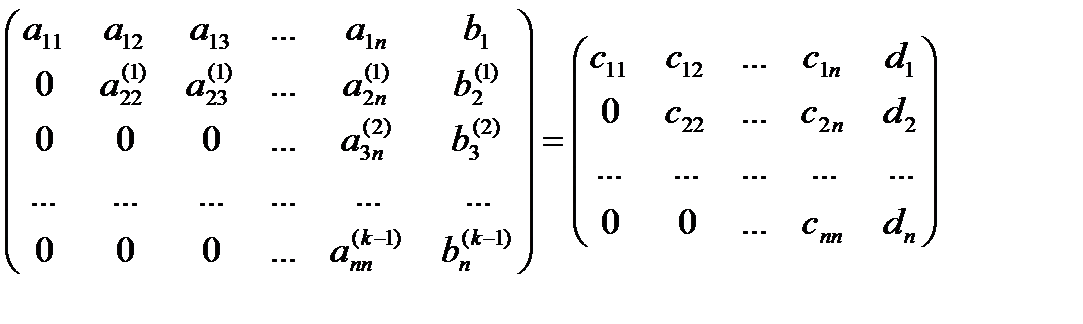Прямой ход закончен. Заметим, что все элементы на главной диагонали отличны от нуля.

Обратный ход

1-й шаг.

Умножим последнюю строку на число 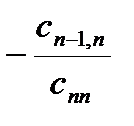и прибавим к предпоследней строке, затем умножим последнюю строку на число 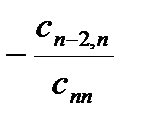и прибавим к (n-2)-й строке, и т.д., т.е. последовательно умножаем последнюю строку на число 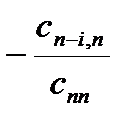и прибавляем к (n-i)-й строке, для i=1, 3, …, n-1.

Получим на первом шаге:

.

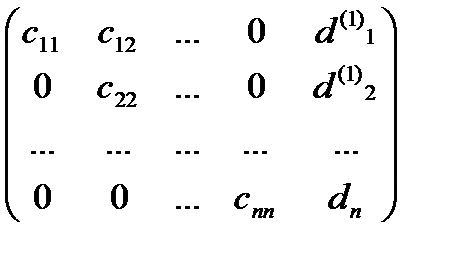k-й шаг

Умножим k-ю строку на число 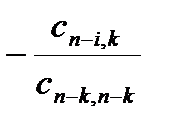и прибавим к i-й строке, для i=k-1, k-2, …, n­-1.

Выполнив n-1 шаг получим:

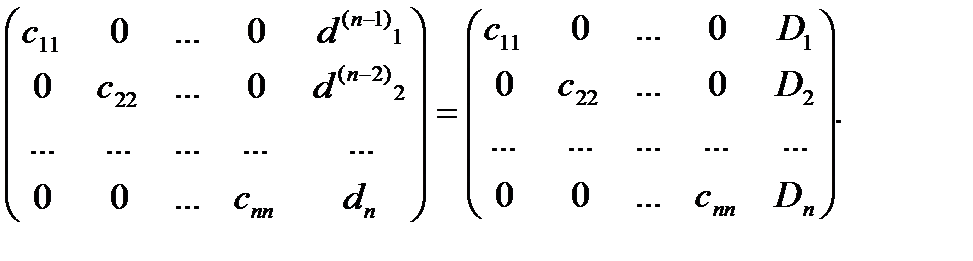
Обратный ход закончен. Решение вычисляем по формулам: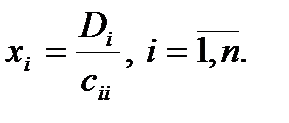

Метод Гаусса решения систем линейных уравнений путем приведения их к трапецеидальному виду. (Ранг системы, базисные и свободные переменные, общее и частное решение, фундаментальная система решений)