Гидростатическое давление и его свойство


Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения.

Как следует из гл. 1, жидкости практически не способны сопротивляться растяжению, а в неподвижных жидкостях не действуют касательные силы. Поэтому на неподвижную жидкость из поверхностных сил могут действовать только силы давления; причем на внешней поверхности рассматриваемого объема жидкости силы давления всегда направлены по нормали внутрь объема жидкости и, следовательно, являются сжимающими. Под внешней поверхностью жидкости понимают не только поверхность раздела жидкости с газообразной средой или твердыми стенками, но и поверхность объема, мысленно выделяемого из общего объема жидкости.

Таким образом, в неподвижной жидкости возможен лишь один вид напряжения напряжение сжатия, т. е. гидростатическое давление.

Рассмотрим основное свойство гидростатического давления: в любой точке жидкости гидростатическое давление не зависит от ориентировки площадки, на которую оно действует, т. е. от углов ее наклона по отношению к координатным осям.

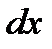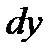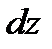Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными , и (рис.2.1). Пусть внутри выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны 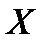, 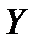и 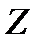. Обозначим через 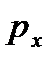гидростатическое давление, действующее на грань, нормальную к оси 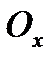, через 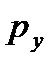— давление на грань, нормальную к оси 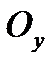, и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через 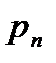, а площадь этой грани через .

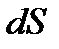Составим уравнение равновесия выделенного объема жидкости сначала в направлении оси 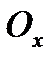, учитывая при этом, что все силы направлены по нормалям к соответствующим площадкам внутрь объема жидкости.

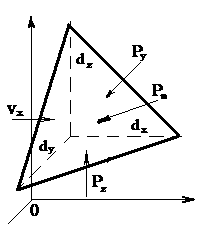
Рис. 1.4 Элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равным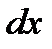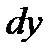и , и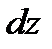

 

Проекция сил давления на ось :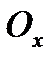

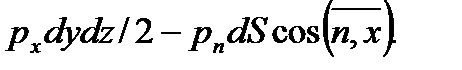
Масса жидкости в тетраэдре равна произведению ее объема на плотность, т. е. 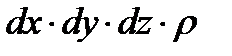, следовательно, массовая сила, действующая на тетраэдр вдоль оси 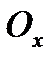, составляет

.

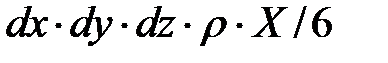Уравнение равновесия тетраэдра запишем в виде:

.

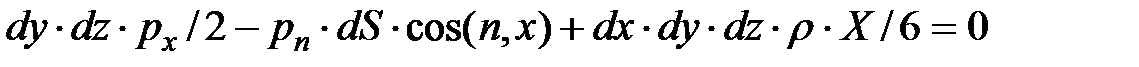Разделив это уравнение на площадь 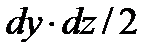, которая равна площади проекции наклонной грани 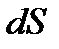на плоскость 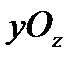, т. е. 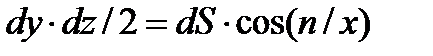, получим

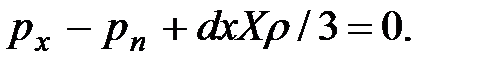
При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель 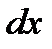, также стремится к нулю, а давления 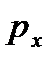и 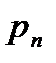остаются величинами конечными. Следовательно, в пределе получим

Аналогично составляя уравнения равновесия вдоль осе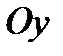й и 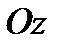, находим

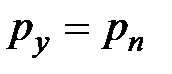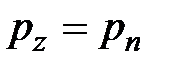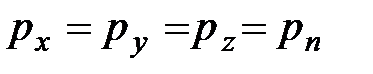, или (2.1)

Так как размеры тетраэдра 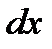, 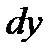и 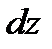взяты произвольно, то и наклон площадки 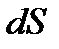произволен и, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково. Это положение можно легко свойства гидростатического давления доказать, основываясь на формулах сопротивления материалов для напряжений при сжатии по двум и трем взаимно перпендикулярным направлениям. Для этого положим в указанных формулах касательное напряжение равным нулю, в результате чего получим

.

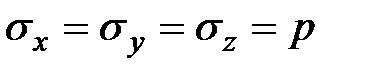Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает.

Основное уравнение гидростатики

Рассмотрим распространенный частный случай равновесия жидкости, когда на нее действует лишь одна массовая сила, сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Если этот объем весьма мал по сравнению с объемом Земли, то свободную поверхность жидкости можно считать горизонтальной плоскостью.

Пусть жидкость содержится в сосуде и на ее свободную поверхность действует давление 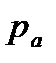. Найдем гидростатическое давление 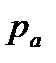в произвольно взятой точке М, расположенной на глубине .

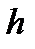Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем высотой 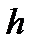. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т. е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикаль:

.

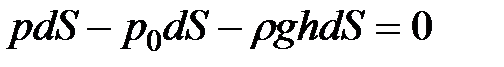Последний член уравнения представляет собой вес жидкости в указанном объеме. Силы давления по боковой поверхности цилиндра в уравнение не входят, так как они нормальны к вертикали. Сократив ,выражение на 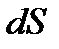,и перегруппировав члены, найдем

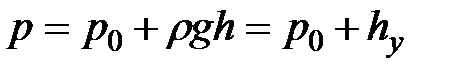(2.2)

Полученное уравнение называют основным уравнением. гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления 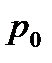на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Величина 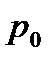является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Давление жидкости, как видно из формулы (2.2), возрастает с увеличением глубины по закону прямой и на данной глубине есть величина постоянная.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня.

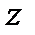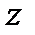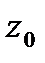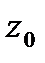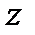Возьмем на произвольной высоте горизонтальную плоскость сравнения, от которой вертикально вверх будем отсчитывать координаты . Обозначив через координату точки М, через координату свободной поверхности жидкости и заменив в уравнении (2.2) h на и , получим

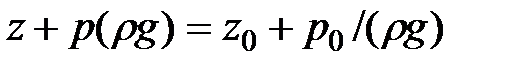. (2.3)

Так как точка М взята произвольно, можно утверждать, что для всего рассматриваемого неподвижного объема жидкости

.

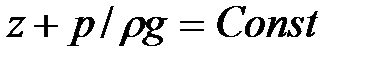Координата 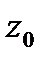называетсягеометрической высотой. Величина 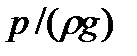имеет линейную размерность и называется пьезометрической высотой. Сумма 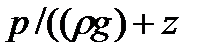) называется гидростатическим напором.

Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.

Те же результаты можно получить путем интегрирования дифференциальных уравнений равновесия жидкости, которые рассмотрены в следующем параграфе.

 


Дата добавления: 2016-05-28; просмотров: 2117;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.009 сек.