Коррекция погрешности линейности обработкой электрического сигнала — результата измерений
Нелинейное преобразование сигнала. Выходное напряжение моста Уитстона или потенциометрической схемы с симметричным питанием является нелинейной функцией изменений сопротивления датчика и определяется выражением
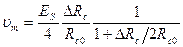
Схема, представленная на рис. 4.6, позволяет нелинейным преобразованием напряжения vm получить напряжение vi, которое является линейной функцией 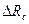 . Напряжение на выходе умножителя напряжений
. Напряжение на выходе умножителя напряжений
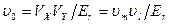 .
.
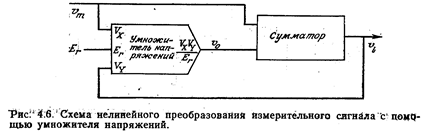
Здесь Ег— опорное напряжение. Коэффициенты усиления каналов умножителя равны соответственно а и b . Выходное напряжение сумматора, осуществляющего суммирование с учетом весовых коэффициентов, равно
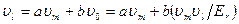
откуда
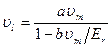
Подставляя выражение vm, получим
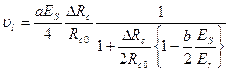
Напряжение vt становится линейной функцией 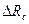 при равенстве единица третьего сомножителя, что достигается выбором соответствующего коэффициента b , а именно:
при равенстве единица третьего сомножителя, что достигается выбором соответствующего коэффициента b , а именно: 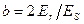
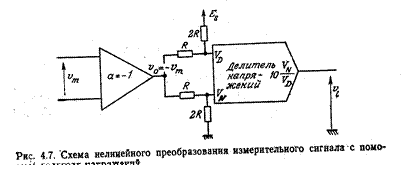
Другая схема нелинейного преобразования результата намерения представлена на рис. 4.7. Ее преимуществом является получение скорректированного результата vl , не зависящего от напряжения питания моста и, следовательно, от флуктуации
этого напряжения.
Схема содержит инвертор и аналоговый делитель, напряжение на выходе которого относительно напряжений Vn и Yd на его входах равно
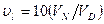
Напряжение на выходе инвертора равно
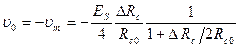
Oбозначая через Ri сопротивление каждого из входов делителя, получнм
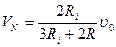 и
и 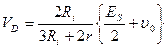
Таким образом, окончательно имеем
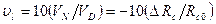
Коррекция результатов измерений введением поправок. Аппроксимация характеристики. Градуировочную характеристику, отражающую связь величин vm и т, можно аппроксимировать многочленом n-й степени
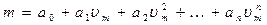
Значения (n+1) постоянных коэффициентов ak можно получить, решая n+1 уравнений, связывающих (n+1) значений vm и m. Такой способ нахождения значений ak не обеспечивает наилучшего и единственного решения, поскольку оно будет зависеть от выбора числа точек аппроксимации. Очевидно, для упрощения решения следует ограничить число членов до приемлемого минимума, определяемого задаваемой погрешностью измерений.
Устройство линеаризации зависимости vm(m) должно формировать напряжение, пропорциональное величине m
т.е. 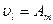
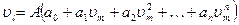
или, обозначая , 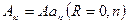
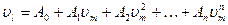
Таким образом, устройство, осуществляющее линеаризацию, можно создать, сочетая умножители, формирующие значении vkm, и сумматоры, осуществляющие их сложение с учетом весовых коэффициентов.
На рис. 4.8 показано аналоговое устройство линеаризации, аппроксимирующее входную функцию (сигнал) многочленом четвертой степени.
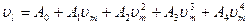
В соответствии с теоремой Мильмана получаем следующие зависимости членов Ak относительно проводимостей, 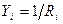 для данной схемы:
для данной схемы:
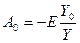
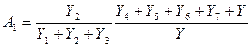
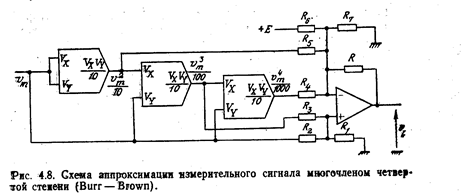
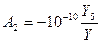
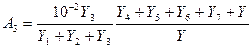
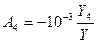
Пример. На основании градуировочной характеристики термопары хромель — константан получено соотношение, которое в диапазоне от -100 до +900°С с погрешностью не хуже 3°С отражает зависимость температуры Т (°С) на измерительном спае (температура опорного спая 0°С) от выдаваемой термопарой термо-э. д. с. е в мВ [11]:
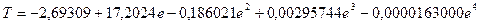
Устройство аппроксимации, приведенное на рис. 4.8, формирует на выходе напряжение Vi, которое численно равно температуре Т при напряжении питания E=10 В и следующих номиналах резисторов (кОм):
R1= 10,00; R2 = 1,340; R3= 77,97;
R4 = 613,5; R5 = 5,376; R6 = 37,13;
R7 = 0,6000; R = 10,00.
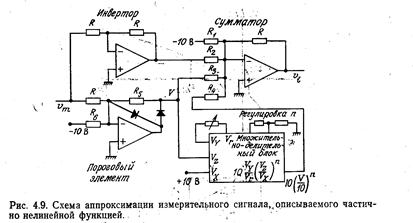
Если градуировочная характеристика аппроксимируется многочленом степени n>2, то более целесообразно применение многофункциональной схемы. Таковая реализована, например, в микросхеме AD433 (изготовитель фирма Analog Devices), ко входам которой прилагаются напряжения Vx, VY, Vz, а на выходе формируется напряжение, пропорциональное величине Vy(Vz/Vx)n, где я регулируется выбором соотношения сопротивления (см. описание схемы на рис. 4.9).
Если функция m=/(um) имеет линейный участок, который заключен между нелинейными участками, то применяют схему ограниченной линеаризации.
Так, например, если для vm>vm1 участок характеристики линеен, т. е. m=a0+a1Vm , то напряжение vl на выходе сумматора
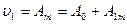
Если при ,vm>vm1 характеристика датчика нелинейна и отклонение предшествующей линейной части нарастает в соответствий с разностью, vm1- vm. то вводимые для коррекции члены должны также соответствовать значениям функции vm1- vm , т.е.
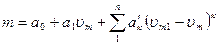 .
.
Устройство линеаризации должно формировать в этом случае напряжение
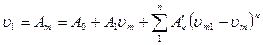 ,
,
Такое устройство должно состоять из одного или нескольких сумматоров, осуществляющих сложение с учетом весовых коэффициентов, пороговой схемы (напряжение V на выходе которой равно нулю для vm>vm1 и пропорционально разности Vm1—vm, когда vm<vml), а также множительно-делительной (многофункциональной) схемы, ко входу которой приложено напряжение V от пороговой схемы.
Схема такого устройства представлена на рис. 4.9. На его выходе формируется напряжение:
при 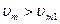
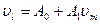
при 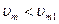
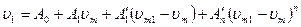
В функции параметров элементов устройства напряжение ,vl выражается соотношением
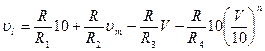
При V=0 для случая vm>vm] имеем , 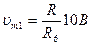 , а для ,
, а для , 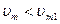
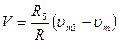
Таким образом, условия линеаризации обеспечиваются надлежащим выбором номиналов компонентов.
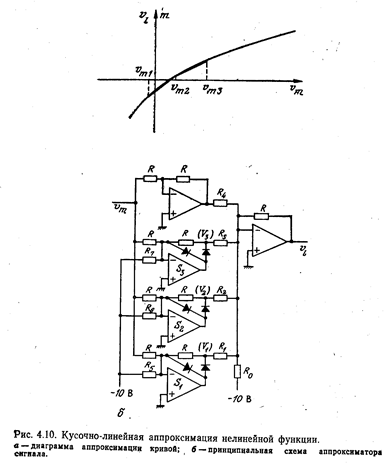
Линеаризация градуировочной характеристики разбиением ее на участки. В общем случае кривая m=f(um) .может быть разбита на конечное число i участков (рис..4.10, а), каждый из которых может быть аппроксимирован двучленом первой степени. 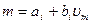
При разбиении кривой на четыре участка, как показано на рис. 4.10, а, справедливы соотношения
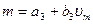
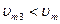
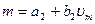
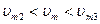
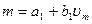
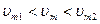
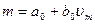
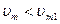
Каждый раз, когда текущее значение vm переходит границу того или иного участка, значение напряжения vi=Am изменяется соответственно наклону данного участка кривой. Это осуществляется с помощью сумматоров, пороги которых соответствуют различным границам vmi, и каждый из которых выдает напряжение Vi равное нулю или пропорциональное vmi —vm в зависимости от того, превосходит или нет значение vm порог сумматора.
На рис. 4.10, б представлено аппроксимирующее устройство, позволяющее осуществить линеаризацию функции, разбитой на четыре участка (см. рис. 4.10, а). Выходное напряжение устройства имеет форму
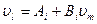 для
для 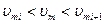
Где 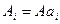 и
и 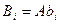
Если границы участков задать в соответствии со значениями
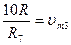
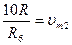
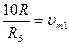
то напряжение vl, на выходе устройства будет равно
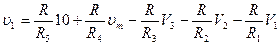
Значения Vi в различных случаях составят:
при
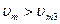
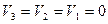
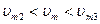
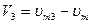
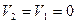
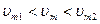
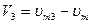
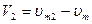
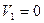
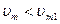
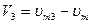
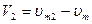
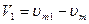
Требуемые номиналы элементов схемы определяются из следующих соотношений:
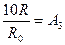
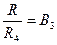
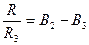
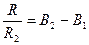
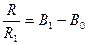
Цифровые методы линеаризации. Их использование, очевидно, требует, чтобы измеряемое напряжение vm было предварительно преобразовано в цифровую форму.
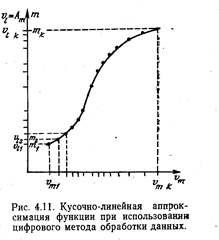
Цифровая система обработки данных (например микро-ЭВМ) позволяет осуществить линеаризацию градуировочной характеристики по программе с приемлемой быстротой. Характеристику vi = f(vm) разбивают на определенное число участков (рис. 4.11), и абсциссы их границ записывают в память машины. Измеряемое напряжение vm сравнивается с этим набором абсцисс: vmi<vm<vmi+1. Когда определяется таким образом номер i участка, запускается программа для расчета vl по алгоритму.
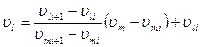
Постоянные коэффициенты 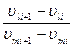 определяющие наклон прямых каждого из участков, должны также храниться в памяти. При такой последовательной обработке данных необходимо учитывать время проведения операций, позволяющее получать результаты с требуемой быстротой.
определяющие наклон прямых каждого из участков, должны также храниться в памяти. При такой последовательной обработке данных необходимо учитывать время проведения операций, позволяющее получать результаты с требуемой быстротой.
Дата добавления: 2016-06-18; просмотров: 1883;











