Принятые в машиностроении знаки поперечных сил и изгибающих моментов

Знаки поперечных сил

Поперечная сила в сече­нии считается положительной, если она стремится развер­нуть сечение по часовой стрелке (рис. 29.4а), если против, — отрицательной (рис. 29.4б).

Знаки изгибающих моментов

Если действующие на участке внешние силы стремятся изогнуть бал­ку выпуклостью вниз, то изгибающий момент считается положительным (рис. 29.5а), если наоборот — отрица­тельным (рис. 29.5б).

Выводы

При чистом изгибе в поперечном сечении балки возникает только изгибающий момент, постоянный по величине.

При поперечном изгибе в сечении возникает изгибающий мо­мент и поперечная сила.

Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, прило­женных к отсеченной части, относительно рассматриваемого се­чения.

Поперечная сила в произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих на отсеченной части, на соответствующую ось.

Пример 2. На балку действует пара сил с моментом т и рас­пределенная нагрузка интенсивностью q. Балка защемлена справа

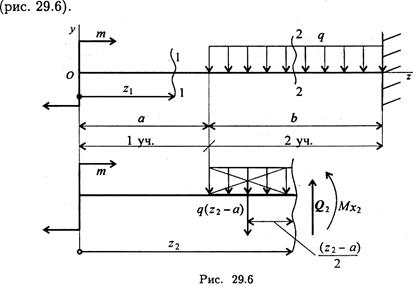
Рассечем балку на участке 1 на расстоянии z₁ от левого края. Рассмотрим равновесие отсеченной части. Из уравнения

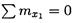
получим:

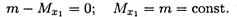
Участок 1 — участок чистого изгиба.

Рассечем балку на участке 2 на расстоянии z₂ > а от края, z₂ — расстояние сечения от начала координат.

Из уравнения ΣFy ⁼ 0 найдем поперечную силу Q_2. Заменя­ем распределенную нагрузку на рассматриваемом участке равнодей­ствующей силой q(z₂ — а).

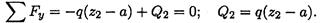
Из уравнения моментов определяем изгибающий момент в сече­нии:

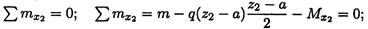
На втором участке возникает поперечный изгиб.

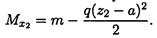
Выводы

При действии распределенной нагрузки возникает поперечная сила, линейно зависящая от координаты сечения.

Изгибающий момент на участке с распределенной нагрузкой меняется в зависимости от координаты сечения по параболическо­му закону.