Двухфакторные и многофакторные уравнения регрессии

Линейное двухфакторное уравнение регрессии имеет вид:

,

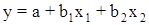где 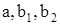- параметры;

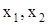– экзогенные переменные;

y – эндогенная переменная.

Идентификацию этого уравнения лучше всего производить с использованием функции Excel ЛИНЕЙН.

Степенное двухфакторное уравнение регрессии имеет вид:

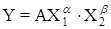
где 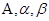- параметры;

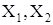– экзогенные переменные;

Y – эндогенная переменная.

Для нахождения параметров этого уравнения его необходимо прологарифмировать. В результате получим:

.

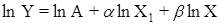
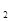Идентификацию этого уравнения также лучше всего производить с использованием функции Excel ЛИНЕЙН. Следует помнить, что мы получим не параметр a, а его логарифм, которое следует преобразовать в натуральное число.

Линейное многофакторное уравнения регрессии имеет вид:

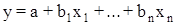
где 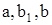_n- параметры;

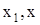_n – экзогенные переменные;

y – эндогенная переменная.

Идентификацию этого уравнения также лучше всего производить с использованием функции Excel ЛИНЕЙН.

Заключение

Объектом изучения эконометрики, как самостоятельного раздела математической экономики, являются экономико-математические модели, которые строятся с учетом случайных факторов. Такие модели называются эконометрическими моделями. Исследование эконометрических моделей проводится на основе статистических данных об изучаемом объекте и с помощью методов математической статистики.

Основными задачами эконометрики являются: получение наилучших оценок параметров экономико-математических моделей, конструируемых в прикладных целях; проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале; создание универсальных и специальных методов для обнаружения статистических закономерностей в экономике.

Для установления статистической зависимости (уравнения регрессии) между изучаемым экономическим показателем (объясняемой переменной) и влияющими на нее факторами (объясняющими переменными) проводится регрессионный анализ. Такой анализ предполагает идентификацию объясняющих переменных, спецификацию формы искомой связи между переменными, определение и оценку конкретных числовых значений параметров уравнения регрессии.

Для выявления тесноты связи между экономическими величинами в уравнении регрессии проводится корреляционный анализ. В ходе корреляционного анализа изучается сила влияния различных причин (последствия линейной регрессии и влияние неучтенных в модели факторов) вариации объясняемой переменной.

Контрольные вопросы к теме №2

1. Определение корреляционной зависимости.

2. Корреляционный и регрессионный анализ.

3. Уравнения регрессии их основные типы и свойства.

4. Определение параметров линейного однофакторного уравнения регрессии.

5. Понятие коэффициента корреляции и его основные свойства.

6. Как определяются погрешности коэффициентов уравнения регрессии.

7. В чем состоит проблема автокорреляции остатков.

8. Сформулируйте критерий Дарбина-Уотсона.

9. Многофакторные уравнения регрессии.