Оптимизационные задачи с линейной зависимостью между переменными

Пусть:

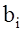- количество ресурса вида i (i=1,2,...,m);

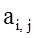- норма расхода i – го ресурса на единицу j – го вида продукции;

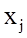- количество продукции вида j (j=1,2,...,n);

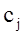- прибыль (доход) от единицы этой продукции (в задачах на минимум – себестоимость продукции).

Тогда оптимизационные задачи линейного программирования (ЛП) в общем виде может быть сформулирована и записана следующим образом:

Найти переменные 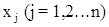, при которых целевая функция

,

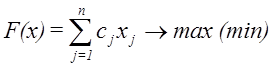была бы максимальной (минимальной), не нарушая следующих ограничений:

,

,

.

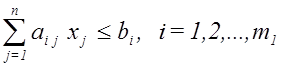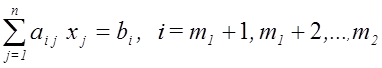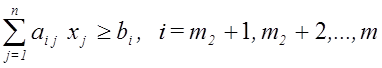Вcе три случая можно привести к так называемой канонической форме, введя дополнительные переменные:

,

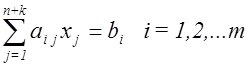k – количество дополнительных переменных,и условие неотрицательности искомых переменных:

.

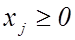В результате решения задачи находится некий план (программа) работы некоторого предприятия. Отсюда и появилось слово «программирование». Слово линейное указывает на линейный характер зависимости как в целевой функции, так и в системе ограничений. Следует еще раз подчеркнуть, что задача обязательно носит экстремальный характер, т.е. состоит в отыскании максимума или минимума (экстремума) целевой функции.