Определение параметров линейного однофакторного уравнения регрессии
Пусть у нас имеются данные о доходах (X) и спрос на некоторый товар (Y) за ряд лет (n)
| ГОД n | ДОХОД X | СПРОС Y |
| x1 | y1 | |
| x2 | y2 | |
| x3 | y3 | |
| ... | ... | ... |
| n | xn | yn |
Предположим, что между X и Y существует линейная взаимосвязь, т.е.
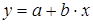
Для того, чтобы найти уравнение регрессии, прежде всего нужно исследовать тесноту связи между случайными величинами X и Y, т.е. корреляционную зависимость.
Пусть:
x 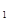 , х
, х 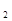 , . . . ,хn- совокупность значений независимого, факторного признака;
, . . . ,хn- совокупность значений независимого, факторного признака;
y 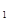 , y
, y  . . . ,yn – совокупность соответствующих значений зависимого, результативного признака;
. . . ,yn – совокупность соответствующих значений зависимого, результативного признака;
n – количество наблюдений.
Для нахождения уравнения регрессии вычисляются следующие величины:
1. Средние значения
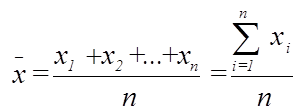 для экзогенной переменной.
для экзогенной переменной.
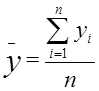 для эндогенной переменной$
для эндогенной переменной$
2. Отклонения от средних величин
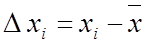 ,
, 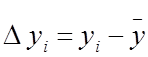 $
$
3. Величины дисперсии и среднего квадратичного отклонения
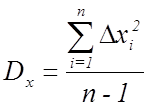 ,
, 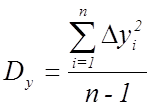 .
.
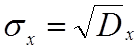
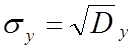
Величины дисперсии и среднего квадратичного отклонения характеризуют разброс наблюдаемых значений вокруг среднего значения. Чем больше дисперсия, тем больше разброс.
4. Вычисление корреляционного момента (коэффициента ковариации):
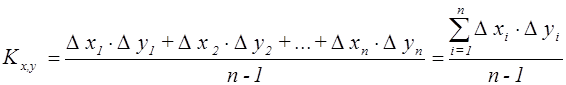
Корреляционный момент отражает характер взаимосвязи между xиy. Если 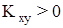 , то взаимосвязь прямая. Если
, то взаимосвязь прямая. Если 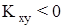 , то взаимосвязь обратная.
, то взаимосвязь обратная.
5. Коэффициент корреляции вычисляется по формуле:
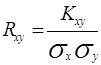 .
.
Доказано, что коэффициент корреляции находится в интервале от минус единицы до плюс единицы ( 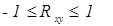 ). Коэффициент корреляции в квадрате (
). Коэффициент корреляции в квадрате ( 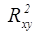 ) называется коэффициентом детерминации.
) называется коэффициентом детерминации.
Если 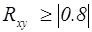 , то вычисления продолжаются.
, то вычисления продолжаются.
6. Вычисления параметров регрессионного уравнения.
Коэффициент bнаходится по формуле:
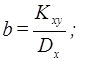
После чего можно легко найти параметр a:
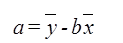
Коэффициенты aиbнаходятся методом наименьших квадратов, основная идея которого состоит в том, что за меру суммарной погрешности принимается сумма квадратов разности (остатков) между фактическими значениями результативного признака 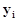 и его расчетными значениями
и его расчетными значениями 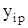 , полученными при помощи уравнения регрессии
, полученными при помощи уравнения регрессии
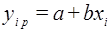 .
.
При этом величины остатков находятся по формуле:
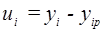 , где
, где
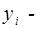 фактическое значение y;
фактическое значение y;
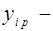 расчетное значение y.
расчетное значение y.
Пример. Пусть у нас имеются статистические данные о доходах (X) и спросе (Y). Необходимо найти корреляционную зависимость между ними и определить параметры уравнения регрессии.
| ГОД n | ДОХОД X | СПРОС Y |
| 10,3 | ||
| 10,5 | ||
Предположим, что между нашими величинами существует линейная зависимость.
Тогда расчеты лучше всего выполнить в Excel, используя статистические функции;
СРЗНАЧ – для вычисления средних значений;
ДИСП – для нахождения дисперсии;
СТАНДОТКЛОН – для определения среднего квадратичного отклонения;
КОРЕЛЛ – для вычисления коэффициента корреляции.
Корреляционный момент можно вычислить, найдя отклонения от средних значений для ряда X и ряда Y , затем при помощи функции СУММПРОИЗВ определить сумму их произведений, которую необходимо разделить на n-1.
Результаты вычислений можно свести в таблицу.
Дата добавления: 2016-05-30; просмотров: 2507;











