Геометрическая интерпретация оптимизационных задач линейного программирования
Пусть необходимо найти оптимальный план производства двух видов продукции (x1 и x2), т.е. такой план, при котором целевая функция (общая прибыль) была бы максимальной, а имеющиеся ресурсы использовались бы наилучшим образом. Условия задачи приведены в таблице:
| Вид продукции | Норма расхода ресурса на единицу продукции | Прибыль на единицу изделия | ||
| А | В | С | ||
| 0,1 | 3,5 | |||
| 0,5 | ||||
| Объем ресурса |
Оптимизационная модель задачи запишется следующим образом:
а) целевая функция:
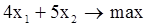
б) ограничения:
2х1 + х2 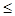 12 (ограничение по ресурсу А);
12 (ограничение по ресурсу А);
0,1х1 + 0,5х2 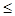 4 (ограничение по ресурсу B);
4 (ограничение по ресурсу B);
3,5х1 + х2 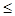 18 (ограничение по ресурсу C).
18 (ограничение по ресурсу C).
в) условие неотрицательности переменных:
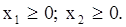
Данную и подобные оптимизационные модели можно продемонстрировать графически (Рис.3.3.).
Преобразуем нашу систему ограничений, найдя в каждом из уравнений x2 , и отложим их на графике. Любая точка на данном графике с координатами x1 и x2 представляет вариант искомого плана. Однако ограничение по ресурсу А сужает область допустимых решений. Ими могут быть все точки, ограниченные осями координат и прямой АА, т.к. не может быть израсходовано ресурса А больше, чем его на предприятии имеется. Если точки находятся на самой прямой, то ресурс используется полностью.
Аналогичные рассуждения можно привести и для ресурсов В и С. В результате условиям задачи будет удовлетворять любая точка, лежащая в пределах заштрихованного многоугольника. Данный многоугольник называется областью допустимых решений.

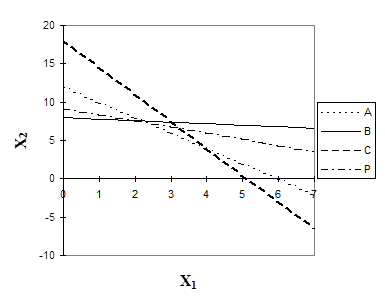
Рис. 3.3. Геометрическая интерпретация оптимизационной задачи
линейного программирования
Однако нам необходимо найти такую точку, в которой достигался бы максимум целевой функции. Для этого построим произвольную прямую 4Х1+5Х2=20, как Х2=4-4/5Х1 (число 20 произвольное). Обозначим эту линию РР. В каждой точке этой линии прибыль одинакова. Перемещая эту линию параллельно ее исходному положению, найдем точку, которая удалена от начала координат в наибольшей мере, однако, не выходит за пределы области допустимых решений. Это точка М0, которая лежит на вершине многоугольника. Координаты этой точки ( 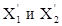 ) и будут искомым оптимальным планом.
) и будут искомым оптимальным планом.
Дата добавления: 2016-05-30; просмотров: 2152;











