Методика використання рівнянь Лагранжа

Другого роду

Перевагою використання рівнянь Лагранжа другого роду до вирішення задач динаміки є єдина методика вирішення задач. Розглянемо порядок роз в’язання надач за допомогою рівнянь Лагранжа другого роду. Він зводиться до наступного:

1) Визначаємо кількість ступенів вільності системи та вибираємо узагальнені координати;

2) Знаходимо узагальнені сили за правилом, описаним у 3.4 б.;

3) Визначаємо кінетичну енергію системи як функцію узагальнених координат і узагальнених швидкостей;

4) Знайдені величини підставляємо у (3.24), отримуємо рівняння Лагранжа другого роду;

5) Спрощуємо та інтегруємо рівняння Лагранжа другого роду;

6) Визначаємо сталі інтегрування із початкових умовзадачі;

7) Знаходимо закон руху точок системи;

8) За найденим законом визначаємо реакції в’язей;

9) Проводимо аналіз результатів обчислень.

Розділ 4. Основи теорії коливань

Коливаннями називаються процеси, що вирізняються тією, чи іншою мірою повторюваності. В залежності від фізичної природи повторюваного процесу розрізняють коливання: механічні, електромагнітні, електромеханічні та ін.

Коливання широко розповсюджені в природі та техніці. В багатьох випадках вони відіграють негативну роль. Разом з тим, коливальні процеси лежать в самій основі різних галузей техніки.

В залежності від характера впливу на коливальну систему розрізняють вільні (власні) коливання, вимушені коливання, автоколивання та параметричні коливання.

Найпростіша коливальна система має два елементи – пружність і масу. При цьому, як найпростіший елемент маси можна використовувати матеріальну точку. У загальному випадку її рух повністю описується заданням радіуса-вектора положення точки як функції часу 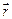або його трьома проекціями на осі (наприклад, декартової системи координат ).

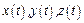4.1. Коливання системи з одним ступенем

вільності

Система, для описання руху якої достатньо знати лише одну функцію часу називається системою з одним ступенем вільності.

Далі розглянемо різні види коливань систем з одним ступенем вільності.

4.1.1.Вільні (власні) коливання

Вільними або власними називаються такі коливання, що відбуваються в системі, наданій самій собі після надання їй поштовху або виведення її з рівноваги.

Прикладом можуть виступати коливання кульки, підвішеної на нитці (маятник), вантажу на пружинці або електричного заряду в коливальному контурі.

В механіці під маятником розуміють тверде тіло, що виконує під дією сили тяжіння коливання навколо нерухомої точки або вісі. Прийнято розрізняти математичний та фізичний маятники.

Приклад 1. Математичний маятник

Математичним маятником називають ідеалізовану систему, що складається з невагомої нерозтяжної нитки, на якій підвішена маса, зосереджена в одній точці. Достатньо добрим наближенням до математичного маятника є невелика важка кулька, підвішена на довгій тонкій ниті.

рис.4.1

Узагальненою координатою для даного випадку є кут відхилення маятника від положення рівноваги q=θ. Запишемо рівняння Лагранжа другого роду:

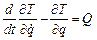або .

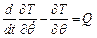Знайдемо кінетичну енергію системи:

,

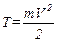де , , , , .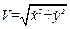

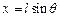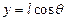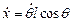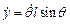Звідси .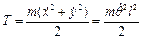

Знайдемо похідні, які входять до рівняння Лагранжа другого роду:

; .

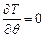Узагальнену силу Q можемо знайти двома способами:

а) Q є коефіцієнтом при варіації узагальненої координати у виразі для елементарної роботи: 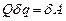або 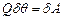в нашому випадку.

Запишемо вираз для елементарної роботи, яку виконує сила тяжіння:

.

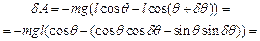
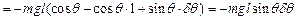Звідси .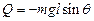

б) 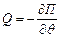, 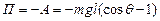- робота сили тяжіння по переміщенню з довільного положення в початкове.

Звідси .

Отже, запишемо рівняння Лагранжа другого роду

; .

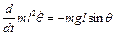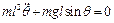Розкладемо функцію синуса в ряд Маклорена 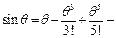… ; для кутів до 20° можемо взяти тільки перший член, отже 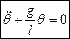- диференціальне рівняння руху математичного маятника.

Приклад 2. Фізичний маятник

Якщо тіло, що коливається неможна представити як матеріальну точку, то маятник називається фізичним. При відхиленні маятника від положення рівноваги на кут j виникає обертаючий момент, що намагається повернути маятник до положення рівноваги.

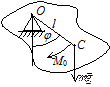
рис. 4.2

Рух тіла визначається узагальненою координатою – кутом повороту відносно положення рівноваги навколо т. О q=j. Запишемо рівняння Лагранжа другого роду:

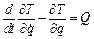або .

Знайдемо кінетичну енергію системи:

.

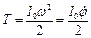Знайдемо похідні, які входять до рівняння Лагранжа другого роду:

; .

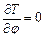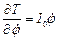Узагальнену силу Q можемо знайти як:

.

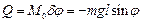Отже, запишемо рівняння Лагранжа другого роду

; .

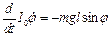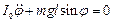Отже 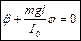- диференціальне рівняння руху фізичного маятника.

Приклад 3. Коливальний контур

Найпростіший електричний коливальний контур складається з катушки та конденсатора, з'єднаних між собою. Вважатимемо,що цей контур з зосередженими ємністю та індуктивністю, або замкненим коливальним контуром.

Коливання в данному контурі являють собою взаємне перетворення електричної енергії конденсатора і магнітної енергії катушки. Під час таких коливань у колі виникає струм, що з плином часу змінює не тільки свою амплітуду, а і напрямок, який двічі на період змінюється на протилежний.

Електричні коливання, що відбуваються під дією процесів в самому коливальному контурі отримали назву власних електричних коливань.

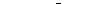
рис. 4.3

В цьому випадку узагальненою координатою будемо вважати заряд q. Коливання описуються наступним рівнянням:

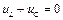, або 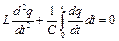, отже ,

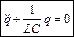де - напруга на індуктивності, 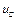- напруга на ємності, L – індуктивність, С - ємність .

Приклад 4. Маса на пружині

Найпростішою коливальною системою в механіці є маса, підвішена на пружині. Система рухається у відсутності тертя. При цьому ми вважаємо, що масою пружини можна знехтувати в порівнянні з масою на пружині, а уся пружність зосереджена в пружині. Це система з зосередженими параметрами.

Коливання в даній системі являють собою взаємне перетворення кінетичної енергії маси і потенціальної енергії деформації пружини.

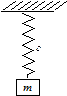
рис.4.4

Узагальненою є абсолютна координата q=x, що описує рух маси т на пружині. Рівняння Лагранжа другого роду:

.

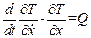Знайдемо кінетичну енергію системи:

.

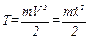Знайдемо похідні, які входять до рівняння Лагранжа другого роду:

; .

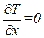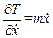рис. 4.5

Узагальнену силу Q можемо знайти як коефіцієнт при варіації узагальненої координати у виразі для елементарної роботи 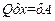або як 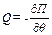, де 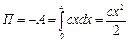- робота сили пружності 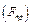по переміщенню з довільного положення в початкове.

Звідси .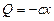

Отже, запишемо рівняння Лагранжа другого роду .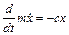

Отримаємо - диференціальне рівняння руху маси на пружині.

Знайдемо вигляд загального диференціального рівняння, яке описує всі чотири розглянуті процеси.

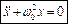, де 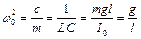. (4.1)

Характеристичне рівняння має вигляд 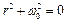. Розв'яжемо його.

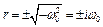; ; звідси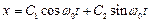

Якщо задані початкові умови 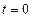, , 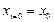, 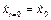то, відповідно, 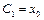, а 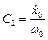. Тоді маємо 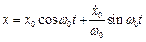. Позначимо 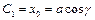та 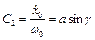, звідси 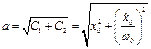та .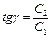

Отже, остаточно можемо записати рівняння колливань, що відповідає розглянутим прикладам 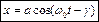, де а – амплітуда, 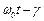- фаза , g - початкова фаза, 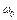- частота власних (вільних) коливань.

рис. 4.6

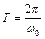- період власних коливань – проміжок часу, за який фаза змінюється на 2p. 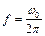- частота в Гц.

Власні коливання є ізохронними, бо їх період коливань не залежить від початкових умов, а залежить лише від параметрів коливальної системи.

4.1.2. Вимушені коливання системи

а) Вимушені коливання в системі при відсутності демпфірування

Вимушені коливання системи – це такі її рухи, які зумовлені дією зовнішньої сили. Математичне моделювання такої ситуації потребує прийняття певної моделі зовнішньої сили. При цьому вважають, що зовнішня сила не залежить ані від узагальненої координати, ані від узагальненої швидкості, тобто від характеру руху системи.

рис. 4.7

Вважатимемо джерело збурюючої сили необмеженим, а саму силу такою, що змінюється за гармонічним законом. Тоді маємо

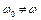, ; (4.2)

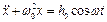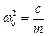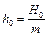, , . (4.3)

Запишемо рівняння Лагранжа другого роду, якщо узагальнена координата q=x

.

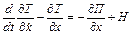Знайдемо розв'язок диференціального рівняння вимушених коливань.

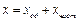; (4.4)

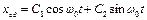, (4.5)

. (4.6)

.

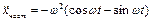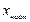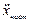Підставимо та в ДР:

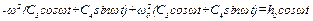
Отримаємо 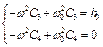, тобто , .

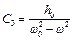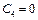Маємо ; ;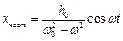

;

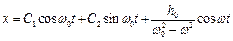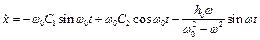Якщо маємо початкові умови t=0, 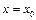, , 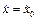то можемо знайти 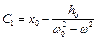та .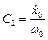

Отже отримали наступне рівняння руху коливальної системи

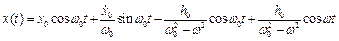. (4.7)

Проаналізуємо вираз (4.7).

1. 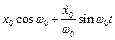- описують вільні коливання системи.

2. 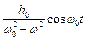- описує вимушені коливання в системі з частотою власних коливань.

3. 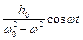- описує вимушені коливання в системі з частотою збурюючої сили.

Якщо маємо початкові умови при t=0 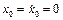, то рівняння руху матиме вигляд

.

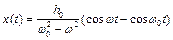Це означає, що коливання системи складається з двох гармонічних рухів (вимушеного та власного), причому амплітуди цих рухів однакові.

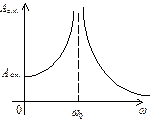
рис. 4.8

Амплітуда вимушених коливань визначається як .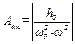

Величина 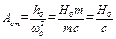називається статичним відхиленням.

Знайдемо вираз для x(t), якщо , тобто розглянемо випадок резонансу. Тоді 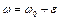, де .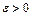

З отриманого результату можемо зробити висновок, що амплітуда на резонансі пропорційна часу.